Tavola forata Montessori per la memorizzazione della divisione. Presentazioni ed esercizi per bambini della scuola primaria.
Per le presentazioni che seguono ho fotografato il materiale prodotto da Montessori 3D di Boboto.
Per poter lavorare con la tavola forata della divisione i bambini devono avere una solida conoscenza dei meccanismi dell’addizione, della sottrazione e della moltiplicazione, perchè la divisione è un’operazione che ha in sé tutte le altre. E’ soprattutto importante che il bambino sappia lavorare con sicurezza con la tavola per la memorizzazione della moltiplicazione.
Trovi tutto il materiale stampabile pronto:
– moduli della divisione versione 1
– moduli della divisione versione 2
– cartellini delle divisioni da svolgere
– tabella di controllo I della divisione
qui:

Gli esercizi collettivi ed i giochi organizzati con le perle dorate danno al bambino una prima rappresentazione materiale della funzione della divisione. Queste attività introduttive vengono poi sostituite con esercizi paralleli svolti con un altro tipo di materiale. Questo materiale si presta all’attività individuale e prepara all’esecuzione dell’operazione scritta. Si tratta di:
– memorizzazione della divisione:
1. attività con la Tavola Forata
2. le tavole della Divisione
– divisione di grandi numeri:
1. struttura dell’operazione (tavole di distribuzione, borsa del quoziente)
2. la grande divisione col divisore di una cifra: (analisi della distribuzione e esecuzione col materiale)
– la grande divisione col divisore di due o più cifre
– la prova della divisione
– calcolo e scrittura della divisione.
Nella pratica della scuola, la divisione coi numeri interi viene esaminata a diversi livelli:
– sistema decimale: funzione della divisione per partizione: dividendo di più cifre e divisore di una o più cifre (gioco del decurione, ecc…)
– gioco dei francobolli: passaggio all’astrazione ed esecuzione dell’operazione, tanto della divisione per partizione quanto della divisione per contenenza; dividendo di più cifre e divisore di una o più cifre; anche divisore con la presenza della cifra zero (203, 230)
– memorizzazione: conoscenza delle combinazioni necessarie e sufficienti; massimo dividendo è 81 e massimo divisore è 9
– divisione col materiale gerarchico: ulteriore passaggio all’astrazione; dividendo di più cifre e divisore di una cifra (piccola divisione o divisione corta) o di più cifre (grande divisione o divisione lunga).
Le divisioni di piccoli numeri (numeri compresi tra 1 e 81) per una cifra (divisore compreso nel limite delle 9 unità semplici), costituiscono il primo degli esercizi paralleli della divisione, accessibile anche ai bambini piccoli.
Per la prima presentazione si usa una tavola forata simile alla Tavola della Moltiplicazione, ma munita di 81 fori invece di 100 (la massima divisione da memorizzare è 81:9=9). Abbiamo inoltre 81 perle verdi (per il dividendo) e una serie di 9 birillini verdi (per il divisore).

La tavola è accompagnata dai Moduli della Divisione, dei foglietti che portano il titolo “Divisione”, e che sono suddivisi in quattro colonne corrispondenti a dividendo, divisore, quoziente e resto. Orizzontalmente il modulo è suddiviso in nove righe: tante quante il numero massimo di divisioni possibili dove il dividendo è nel limite di 81 e divisore e quoziente non superano il 9.
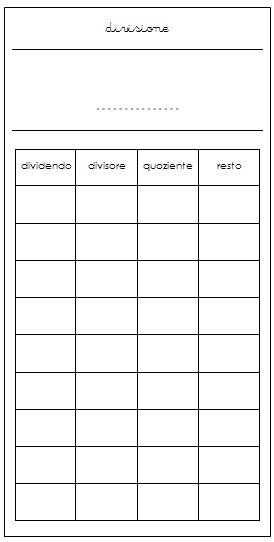
Tavola forata Montessori per la memorizzazione della divisione
Moduli della Divisione versione 1
Una seconda versione di questi moduli prevede nella seconda colonna l’elenco in ordine decrescente di tutti i divisori possibili (da 9 a 1).
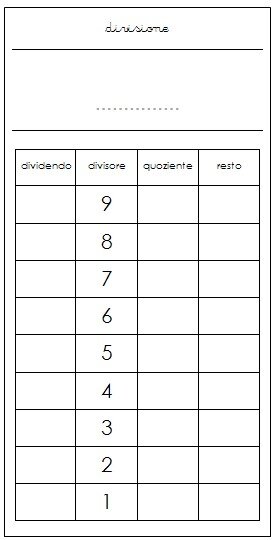
Tavola forata Montessori per la memorizzazione della divisione
Moduli della Divisione versione 2
La differenza tra le due versioni di moduli risiede nel fatto che con la prima il bambino costruisce le divisioni e si arresta su quella il cui quoziente sarà maggiore di 9. Con la seconda il bambino compila le parti mancanti solamene di quelle divisioni il cui quoziente non supera il 9, mentre cancella quelle che non sono utilizzabili per il suo lavoro.
Ogni bambino dispone di 81 moduli, raccolti in una busta o rilegati in forma di libretto.
Si comincia prendendo in considerazione le 81 perle verdi nella loro scatola e i 9 birillini che si dispongono lungo la striscia verde che in alto limita la tavola. Spiegheremo ai bambini che ogni birillo deve ricevere la stessa quantità di perle.

L’operazione inizia assegnando una perla a ciascun birillo e, conclusa una prima distribuzione, si continuerà fino all’esaurimento del dividendo.

Poi si conta il numero delle righe di 9 perle ciascuna che si sono potute organizzare: ce lo indicherà anche il corrispondente numero, scritto sulla colonna a sinistra della tavola.

Il bambino, sul modulo, sotto la parola dividendo scriverà 81, sotto la parola divisore 9, sotto quoziente ancora 9 e sotto resto 0. I termini dell’operazione, ogni volta che ci si imbatte in una divisione esatta, vengono evidenziati sottolineandoli con un colore brillante.
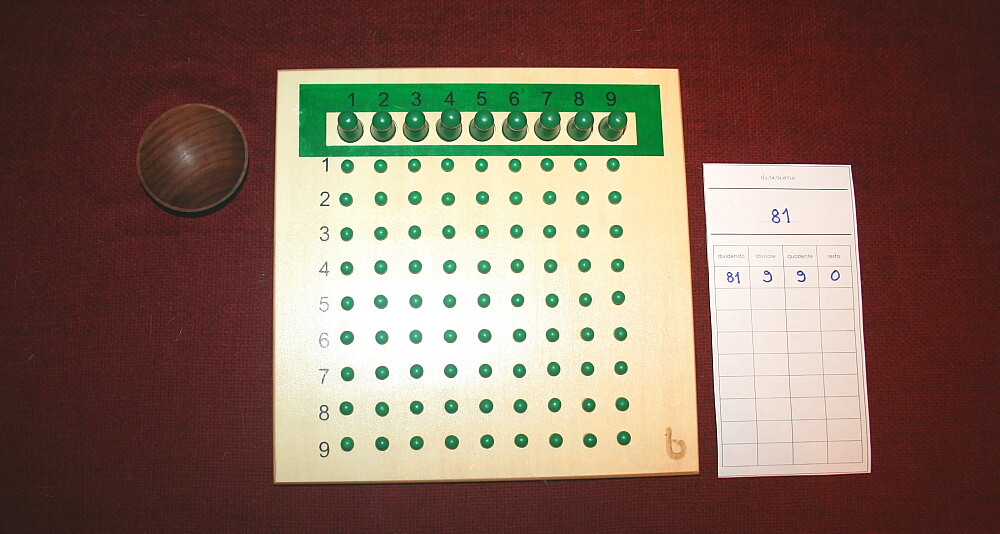
Dopo aver dato al bambino l’indicazione che nessun quoziente e nessun divisore possono essere maggiori di 9, e che nessun resto può essere maggiore o uguale al divisore. Così, dopo aver completato la tavola, il bambino si accerta che con 81 perle non può organizzare nessun’altra divisione.
Rimuoviamo una perla, riducendo il dividendo a 80, e ripetiamo la distribuzione.
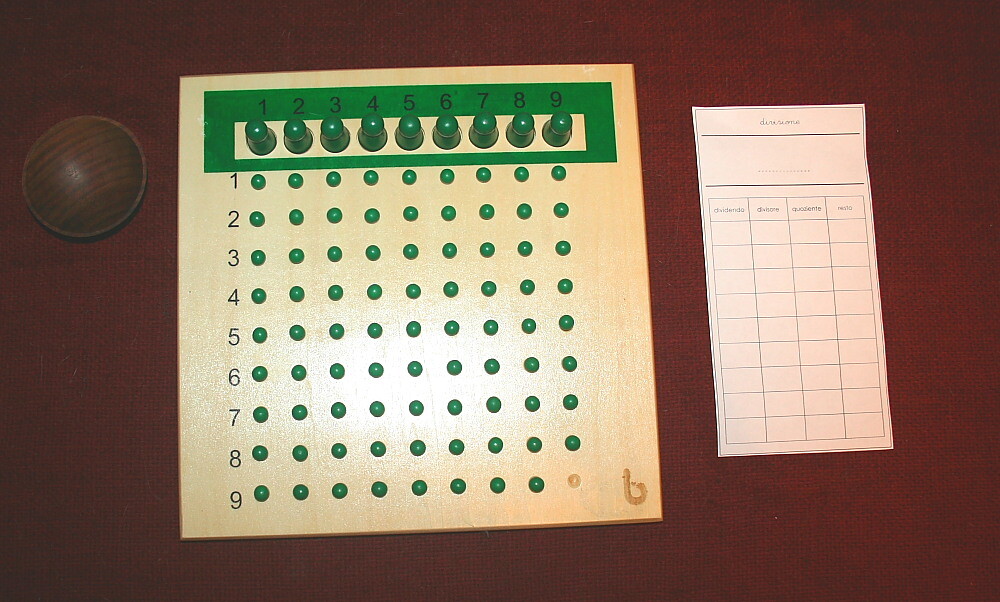
Il bambino calcola che 80:9 è uguale a 8, ma gli rimangono 8 perle. Scrive sul modulo. A questo punto rimuove un birillino, riducendo così a 8 il divisore.

Ripetendo la distribuzione scopre che, nonostante abbia dato 9 perle ad ognuno degli 8 birillini, gliene rimangono ancora 8, che è una quantità di perle uguale al divisore. Per questo non si può, con 80 perle, procedere oltre.
L’esercizio riprende, rimuovendo una perla (ora sono 79), ma ricollocando al suo posto il nono birillino. E così via.

Il procedimento seguito si può così riassumere:
– partendo da un dividendo di 81 perle, suddividerlo successivamente per tutti i divisori possibili da 9 a 1, al fine di ottenere quozienti non superiori a 9
– poi, togliere una perla e suddividere il nuovo dividendo come sopra
– procedere così togliendo sempre una perla e suddividendo tutti i nuovi dividendi per tutti i divisori da 9 a 1.
A conclusione dell’esplorazione, il bambino avrà organizzato moltissime divisioni, delle quali è necessario memorizzare soltanto quelle esatte (che saranno in totale 81).
Ogni volta il bambino scrive sui moduli come già spiegato, ma tenendo presente che per ogni nuovo dividendo si usa un nuovo modulo.
Sempre riguardo ai moduli, usando quelli presentati come seconda versione si hanno tre casi:
– il modulo risulta riempito completamente: col dividendo 9 ed è l’unico caso (da 9:9 a 9:1)
– il modulo risulta riempito soltanto nella parte superiore: cioè là dove i divisori sono alti; per esempio col dividendo 56 (da 56:9 a 56:6)
– il modulo risulta riempito soltanto nella parte inferiore: cioè là dove i divisori sono bassi; per esempio col dividendo 5 (da 5:5 a 5:1)
Usando invece i moduli nella prima versione, il bambino, per ogni dividendo, prende in considerazione soltanto i possibili divisori. E, per questo, è la versione di moduli che si preferisce utilizzare.
Tutti gli altri esercizi che derivano da questa presentazione si sviluppano su punti di coscienza successivi da porre all’attenzione del bambino:
– dalle sole divisioni esatte o complete, alla divisione come operazione inversa della moltiplicazione
– dai divisori possibili di un numero fino al concetto di divisibilità.
L’età per questo genere di attività si situa intorno ai 6 anni.
___________________________
Tavola forata Montessori per la memorizzazione della divisione
Presentazione 1 – eseguire divisioni con la tavola forata
Materiali:
– tavola forata per la memorizzazione della divisione
– una ciotola
– cartellini delle divisioni da svolgere (o cartellini bianchi e penna nera) in una scatolina
– tavolo o tappeto.
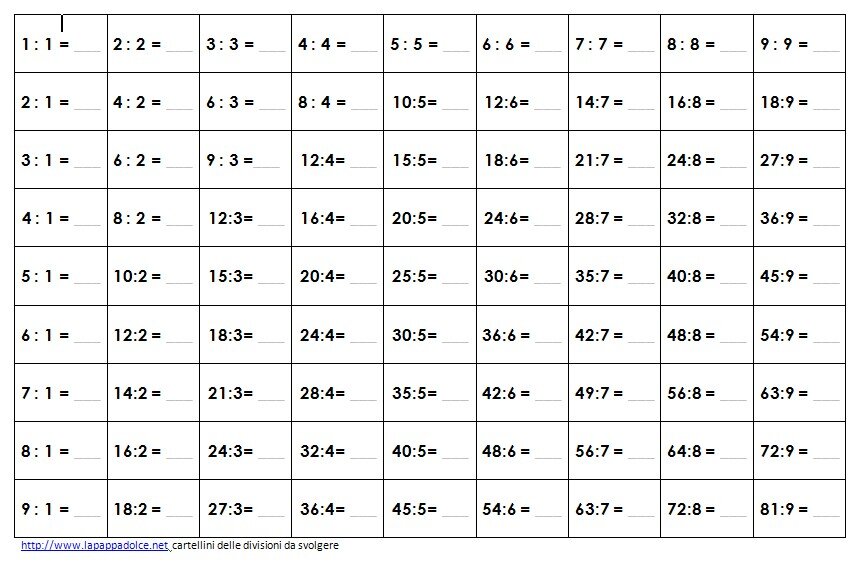
Tavola forata Montessori per la memorizzazione della divisione
cartellini delle divisioni da svolgere

Presentazione:
– invitiamo il bambino ad unirsi a noi nell’esercizio dicendo: “Oggi ti mostrerò un nuovo modo per fare le divisioni” e chiediamogli di srotolare un tappeto
– andiamo allo scaffale della matematica, indichiamo il materiale e diciamo: “Questa è la tavola forata della divisione”
– portiamo il materiale al tappeto
– mettiamo la tavola al centro del piano di lavoro ed esaminiamola col bambino
– indichiamo i fori lungo il margine superiore che servono per i birilli e che ci indicano il divisore
– indichiamo i fori più piccoli sulla tavola, dove metteremo le perle che indicano il dividendo
– scegliamo una divisione tra i cartellini delle divisioni pronte, oppure scriviamola su un cartellino bianco

– diciamo al bambino che per questo esercizio abbiamo due regole: il risultato non può essere più grande di 9, e il resto non può essere uguale o più grande del divisore
– contiamo le perle verdi che rappresentano il dividendo e mettiamole in una ciotola
– mettiamo i birilli che rappresentano il divisore lungo il margine superiore della tavola

– distribuiamo le perle procedendo sempre da sinistra a destra sotto ai birilli

– poi distribuiamo la seconda fila di perle

– e continuiamo in questo modo finché tutte le perle non saranno distribuite equamente sotto ad ogni birillo

– chiediamo: “Quante perle ha ricevuto ogni birillo?”
– il bambino risponde e registra l’operazione e il risultato sul quaderno

– chiediamo al bambino di prendere una nuova divisione da svolgere e di leggerla a voce alta
– ripetiamo il processo
– al termine chiediamo al bambino se gli piacerebbe fare una divisione da solo, quindi prendiamo una divisione da svolgere e leggiamola a voce alta
– il bambino completa il processo.
Note:
– per i primi esercizi è meglio scegliere divisioni senza resto.
__________________________
Tavola forata Montessori per la memorizzazione della divisione
Presentazione 2 – moduli per la divisione
Materiale:
– tavola forata per la divisione
– moduli per la divisione sciolti o rilegati in forma di libretto
– tavolo o tappeto
– una ciotola.
Presentazione:
– esaminiamo col bambino i moduli. Indichiamo l’intestazione, su cui è scritta la parola ‘divisione’ e le intestazioni delle quattro colonne: dividendo, divisore, quoziente, resto
– prendiamo un modulo e scriviamo come intestazione 81
– chiediamo al bambino di contare 81 perle e di metterle nella ciotola
– diciamo al bambino che vogliamo distribuire le 81 perle tra 9 birilli
– ricordiamo le due regole della tavola forata: il risultato non può essere più grande di 9, e il resto non può essere uguale o più grande del divisore
– mettiamo i 9 birilli lungo il margine superiore della tavola
– scriviamo sul modulo la prima divisione, cioè 81 (dividendo) 9 (divisore)
– distribuiamo le 81 perle sulla tavola procedendo sempre da sinistra a destra per completare le file e scendendo poi alla fila successiva
– indichiamo la tavola: distribuendo 81 perle tra 9 birilli, ogni birillo ha ricevuto 9 perle
– scriviamo 9 nella colonna quoziente e rileggiamo per intero l’operazione che abbiamo scritto sul modulo
– la ciotola delle perle è vuota: questo significa che il resto è 0, quindi scriviamo 0 sul modulo
– diciamo al bambino che le divisioni senza resto sono le più importanti di tutte, e che per ricordarle possiamo sottolineare sul modulo

– togliamo le 81 perle dalla tavola e rimettiamole nella ciotola
– diciamo al bambino che ora proveremo a distribuire le 81 perle tra 8 birilli invece che 9, quindi togliamo un birillo dalla tavola
– ricordiamo le due regole della tavola forata: il risultato non può essere più grande di 9, e il resto non può essere uguale o più grande del divisore
– distribuiamo le perle tra gli otto birilli, come abbiamo già fatto nella divisione precedente

– contiamo le perle avanzate nella ciotola: sono 9! Siccome 9 supera il divisore, che è 8, e siccome non abbiamo spazio sulla tavola per queste perle avanzate, non possiamo eseguire questa divisione con la tavola
– rimettiamo le 81 perle nella ciotola e proviamo a dividerle per 7, poi ripetiamo anche dividendole per 6 e se il bambino lo desidera per gli altri numeri inferiori
– osserviamo coi bambini che il resto diventa sempre più grande se il dividendo diventa sempre più piccolo
– per questo motivo sul modulo dell’81 possiamo scrivere soltanto 81:9=9, resto 0
– liberiamo la tavola, prendiamo un nuovo modulo e scriviamo nell’intestazione 80
– contiamo 80 perle e mettiamole nella ciotola
– diciamo al bambino che vogliamo distribuire le 80 perle tra 9 birilli
– ricordiamo le due regole della tavola forata: il risultato non può essere più grande di 9, e il resto non può essere uguale o più grande del divisore
– mettiamo i 9 birilli lungo il margine superiore della tavola
– scriviamo sul modulo la prima divisione, cioè 80 (dividendo) 9 (divisore)
– distribuiamo le 80 perle sulla tavola procedendo sempre da sinistra a destra per completare le file e scendendo poi alla fila successiva
– indichiamo la tavola: distribuendo 80 perle tra 9 birilli, ogni birillo ha ricevuto 8 perle
– scriviamo 8 nella colonna quoziente e rileggiamo per intero l’operazione che abbiamo scritto sul modulo
– la ciotola delle perle ne contiene 8: questo significa che il resto è 8, quindi scriviamo 8 sul modulo
– anche con l’80 non possiamo continuare oltre il 9 perchè il resto supererebbe il 9
– liberiamo la tavola, prendiamo un nuovo modulo e scriviamo nell’intestazione 79
– contiamo 79 perle e mettiamole nella ciotola
– diciamo al bambino che vogliamo distribuire le 79 perle tra 9 birilli
– ricordiamo le due regole della tavola forata: il risultato non può essere più grande di 9, e il resto non può essere uguale o più grande del divisore
– mettiamo i 9 birilli lungo il margine superiore della tavola
– scriviamo sul modulo la prima divisione, cioè 79 (dividendo) 9 (divisore)
– distribuiamo le 79 perle sulla tavola procedendo sempre da sinistra a destra per completare le file e scendendo poi alla fila successiva
– indichiamo la tavola: distribuendo 79 perle tra 9 birilli, ogni birillo ha ricevuto 8 perle
– scriviamo 8 nella colonna quoziente e rileggiamo per intero l’operazione che abbiamo scritto sul modulo
– la ciotola delle perle ne contiene 7: questo significa che il resto è 7, quindi scriviamo 7 sul modulo
– anche col 79 non possiamo continuare oltre il 9 perchè il resto supererebbe il 9

Note:
– dopo aver dato queste indicazioni, il bambino continua a lavorare col materiale e gli altri dividendi, registrando sempre il suo lavoro e sottolineando sempre le divisioni senza resto
– non è necessario che lavori con tutti i dividendi, ciò che importa è che comprenda il procedimento
– se il bambino non lo ha notato da solo, dopo aver svolto un certo numero di esercizi con i moduli possiamo attirare la sua attenzione sui rapporti tra dividendo, divisore e quoziente, ad esempio:
12 : 4 = 3 e 12 : 3 = 4.
_______________________
Tavola forata Montessori per la memorizzazione della divisione
Presentazione 3 – tavola di controllo della divisione
Materiale:
– tavola forata per la divisione
– cartellini delle divisioni da svolgere
– tabella di controllo I della divisione.
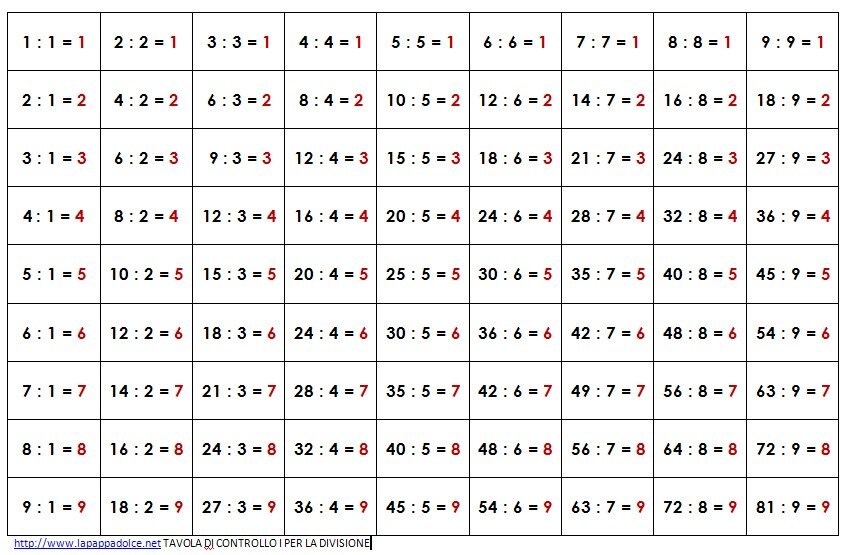
Tavola forata Montessori per la memorizzazione della divisione
tabella di controllo I della divisione
Presentazione:
– scegliamo una divisione,
– copiamo la divisione sul quaderno

– stabiliamo il dividendo contando le perle verdi e mettendole nella ciotola
– stabiliamo il divisore mettendo sulla tavola i birilli verdi corrispondenti

– distribuiamo il dividendo
– registriamo il numero di perle assegnate a ogni birillo (quoziente)

– controlliamo il risultato sulla tavola di controllo

– togliamo i birilli e le perle
– scegliamo un’altra divisione
– eseguiamola come fatto con la prima
– controlliamo sulla tavola di controllo il risultato.
________________________________
Tavola forata Montessori per la memorizzazione della divisione
Esercizi con la tavola forata della divisione
Scopo:
– memorizzare le divisioni
– acquisire familiarità con i modi in cui i numeri possono essere divisi
– dimostrare che ogni numero è divisibile e solo per alcuni numeri
– mostrare la relazione tra moltiplicazione e divisione
– fare esperienze concrete con la divisione utilizzando come divisore massimo il 9
– sperimentare a livello sensoriale la relazione inversa tra divisione e moltiplicazione.
Controllo dell’errore:
– i birilli e i fori per le perle possono fungere da controllo dell’errore
– la tavola di controllo
– la tavola I della divisione.
Età:
– dai 5 e mezzo agli 8 anni.
________________________________
Tavola forata Montessori per la memorizzazione della divisione
DIY
Questo è un esempio di tavola stampabile usata con i Lego:

Tavola forata Montessori per la memorizzazione della divisione

