imparare coi bambini
IL FIORE E LA FECONDAZIONE tavole e schede pronte per la stampa e il download gratuito, in formato pdf, per bambini della scuola primaria. Aggiungo all’articolo illustrazioni e didascalie che possono essere utili per preparare un cartellone da parete.
Trovi la tavola riassuntiva della classificazione delle piante qui:
_________________________________
IL FIORE E LA FECONDAZIONE tavole e schede
Questo è il materiale pronto in formato tavola:
E questo lo stesso materiale in formato scheda:
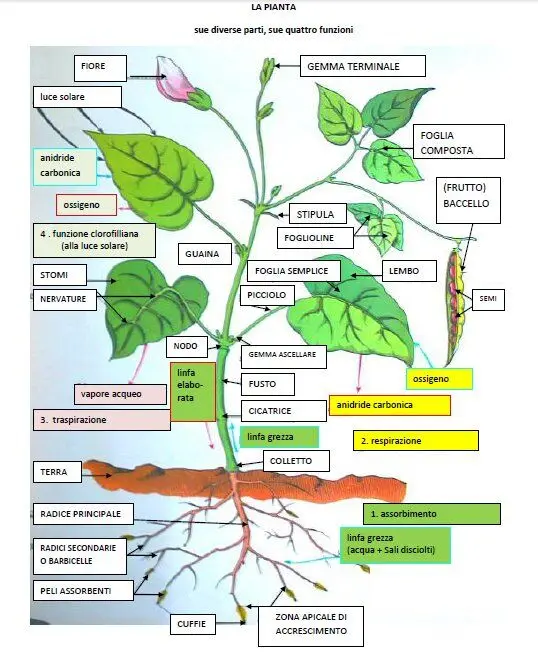
PARTI DELLA PIANTA tavole pronte per la stampa e il download , in formato pdf, per bambini della scuola primaria.
Trovi la tavola riassuntiva della classificazione delle piante qui:
_________________________________
La pianta utilizzata ad esempio è quella del fagiolo. La tavola, oltre ad indicare le principali parti di cui si compone una pianta, ne illustra anche le quattro principali funzioni, che sono:
– assorbimento
– respirazione
– traspirazione
– funzione clorofilliana.
Questa è la tavola contenente tutte le didascalie:
Questo è invece la tavola da compilare:
ALGHE tavole riassuntive e schede pronte per la stampa e il download gratuito, in formato pdf, per bambini della scuola primaria. Aggiungo all’articolo illustrazioni e didascalie che possono essere utili per preparare un cartellone da parete.
Trovi la tavola riassuntiva della classificazione delle piante qui:
_________________________________
Questo è il materiale pronto in formato tavola:
E questo lo stesso materiale in formato scheda:
ALGHE tavole riassuntive e schede
LA CLASSIFICAZIONE DELLE PIANTE scheda riassuntiva pronta per la stampa e il download in formato pdf, per bambini della scuola primaria.
Le piante si suddividono in due grandi categorie: le piante con fiore e le piante senza fiore.
Tra le piante con fiore troviamo quelle con foglie a nervature non parallele e quelle a nervature parallele.
Tra le piante con foglie a nervature non parallele troviamo tutte le piante che presentano fiori completi, cioè con stami, petali, sepali e pistilli, che sono:
– crucifere
– rosacee
– leguminose
– ombrellifere
– composte
– solanacee
e piante che presentano due qualità di fiori sullo stesso albero, che sono gli alberi forestali come la quercia.
trovi il materiale sulle crocifere qui:
trovi il materiale sulle rosacee qui:
Ho utilizzato la pianta del fagiolo in queste tavole:
– parti della pianta e funzioni:
– il fiore e la fecondazione:
– la germinazione:
trovi il materiale sulle ombrellifere qui:
trovi il materiale sulle composte qui:
trovi in materiale sulle solanacee qui:
trovi il materiale sugli alberi forestali (cupolifere) qui:
Tra le piante con foglie a nervature parallele troviamo:
– liliacee
– graminacee
trovi il materiale sulle liliacee qui:
trovi il materiale sulle graminacee qui:
Le piante senza fiore comprendono:
– felci: con radici, fusto, foglie
– muschi: con fusto e foglie, senza radici
– alghe: ne radici ne fusto ne foglie
trovi il materiale sulle felci qui:
trovi il materiale sui muschi qui:
trovi il materiale sulle alghe qui:
I funghi non sono da considerarsi piante.
trovi il materiale sui funghi qui:
LA CLASSIFICAZIONE DELLE PIANTE scheda riassuntiva
Disegni da colorare FIORI con scheda didattica e nomenclature Montessori per bambini della scuola primaria, anche stampabili in formato pdf.
Le carte delle nomenclature sono queste:
I fiori più comuni dei nostri prati e dei nostri giardini
Per mettersi bene in vista questo fiore ha colorato i suoi petali di colori diversi l’uno dall’altro. Le striature che convergono verso il centro indicano agli insetti la strada da seguire per raggiungere il nettare e, naturalmente, gli stami e i pistilli.
I ranuncoli levano la loro corolla su uno stelo eretto, ornato di foglie palmate come le dita di una mano; sono detti anche “botton d’oro” perchè sembra abbiano racchiuso, nei loro cinque petali, tutto il colore del prezioso metallo.
I ciclamini hanno radice grossa, rotonda, carnosa; foglie leggermente ovali e graziosamente screziate di un verde più chiaro; fiori rosei, profumati, se cresciuti in località di alta montagna. Nell’Italia centrale e meridionale, i ciclamini hanno foglie e fiori più grandi; ma i fiori sono più pallidi e senza profumo.
La petunia è una pianta vivace che vive parecchi anni. Ha foglie pelose e fitte, fiori a forma di campana di vari colori: bianchi, rossi, violacei o azzurri.
La zinnia proviene dal Messico ed è un fiore molto diffuso. I suoi fiori doppi o semplici, di svariatissime tinte, sbocciano solitari sulla cima di ogni ramoscello. Questo fiore adorna tutti i giardini, anche i più poveri, per la sua grande facilità di crescita e di coltivazione.
La serenella (o lillà) è molto diffusa nei giardini perchè si adatta ad ogni terreno e ad ogni posizione. Fiorisce in pannocchie all’estremità dei rami ed emette un soave profumo. I fiori bianchi o lilla sono semplici o doppi.
L’ortensia è originaria dell’Asia. E’ un arboscello di piccole dimensioni, con foglie verdi, lucenti. Sulla cima di ogni ramo porta grandissimi fiori, disposti a corimbo, vivacissimi.
Le bocche di leone sono così chiamati per la loro forma e per la caratteristica di aprirsi come una bocca se premuti leggermente ai lati; sono fiori riuniti all’estremità di steli rigidi; i colori vanno dal bianco al giallo, all’arancione, al rosa salmone, al rosa vivo, al cremisi intenso. Spesso in un unico fiore sono riuniti più colori, con un effetto curioso e piacevole.
Le peonie sono assai decorative e disposte in gran quantità nei giardini per la varietà dei colori e per la facilità di coltura. E’ un fiore di lunga durata e spesso di delicato profumo.
I garofani hanno steli diritti, fiori con corolle dei colori più vari: rosa, porporino, rosso, carneo, bianco. I fiori sono talora semplici, talora doppi, o di un solo colore o striati o punteggiati. Molte specie di questo fiore sono state introdotte dalla Cina e dal Giappone. Da questo fiore si ottengono prodotti di profumeria.
Le begonie hanno eleganza e bellezza di fogliame, magnificenza e durata di fioritura, estrema facilità di coltura. Le specie sono circa ottocento; provengono principalmente dall’America meridionale e dall’Asia.
Graziosissima, coi rami rossicci, la fucsia può prendere forma di alberello, di piramide o di ombrello. Le foglie sono verdi nella parte superiore, sono rosseggianti al di sotto. I fiori pendono come ciondoli da un gambo leggero, che si china al loro peso. Le tinte dei fiori sono bellissime; fra esse spicca sempre un rosso vivo, che contrasta con un violetto splendido.
La margherita bianca o semplice è preferita alla doppia ed alla gialla. In terra e nei vasi forma un alberello regolare con foglie belle, tagliuzzate, d’un verde chiaro. I suoi fiori hanno i petali candidi, lunghi, distesi regolarmente attorno al centro giallo del fiore; sembrano stelle raggianti e stanno bene nei vasi sui balconi.
Il mughetto è anche detto “giglio delle valli” ed ha belle foglie lucenti. Dal cespo verdissimo e compatto delle foglie sorgono gli steli dei fiori, graziosi e diritti, carichi di candide campanelle. Questi fiori emanano tutto attorno un soavissimo profumo.
Le foglie sempreverdi dell’erica porporina spuntano a tre a tre dallo stelo; sono sottili, accartocciate per il lungo, così che sembrano aghi; i fiori color carminio, disposti ad intervalli sulla parte superiore dello stelo, pendono un poco l’uno sull’altro; hanno quattro sepali distinti; ma i petali, riuniti, formano una specie di campanellina rossa, ovale, la cui apertura ha quattro lobi. Il pistillo è così lungo che sporge dalla bocca del fiore; intorno al pistillo, ma ben dentro al fiore, stanno otto stami.
La ginestra cresce in cespugli fitti e con i suoi bei fiori giallo lucente mette allegria; bisogna osservarla da vicino per trovare qualche foglia su questa pianta, perchè tanto le foglie quanto i ramoscelli si sono tutti tramutati in punte acute. I fiori sono simili a quelli del pisello, di cui le ginestre sono parenti. Esiste una ginestra nana che cresce appena a fior di terra, e per le caviglie è tutt’altro che piacevole. Le ginestre contengono i semi entro piccoli baccelli bruni che, quando sono maturi, si spaccano per il lungo come quelli dei piselli; essi sono granellini duri, verde – bruni.
L’orchidea delle farfalle ha due grandi foglie oblunghe vicine al terreno, uno stelo altro da 30 a 40 cm, intorno a cui sembrano raggruppate in quantità farfalline bianchicce e piumose. Se la osserviamo nell’ora del crepuscolo, la somiglianza tra i suoi fiori e le farfalle è anche maggiore; ed è molto probabile che le farfalle vere vengano più facilmente intorno a questa pianta, ingannate appunto dal suo aspetto.
La pervinca ha un gambo strisciante con stoloni. I fiori sono a cinque petali, di colore blu chiaro. Cresce nei boschi radi e nelle siepi.
Se possono esservi utili, qui i disegni da colorare stampabili gratuitamente in formato pdf:
______________________
Tavola con asticine dell’addizione e tavole di controllo stampabili. Il lavoro necessario a calcolare qualsiasi addizione si incentra sempre intorno al 10. Le addizioni parziali dei gruppi possono rimanere al di sotto della decina, raggiungerla o superarla. Per completare l’esercizio col tavoliere delle asticine, si offre un materiale scritto che conduce il bambino alla memorizzazione necessaria per il calcolo rapido.
In questo articolo trovi la descrizione dettagliata di tutte le tavole per l’addizione predisposte dalla Montessori, la tombola delle addizioni, i cartellini ed i moduli da compilare; mentre trovi tutto il materiale pronto per la stampa qui:
Il tavoliere delle asticine è in due versioni:
– piccola
– grande.
Oltre al tavoliere il materiale comprende tutte le tavole di controllo previste da Maria Montessori, compresa la tombola dell’addizione:
– moduli per l’esercizio scritto
– cartelli delle operazioni per le addizioni
– tavola I: questa tavola rappresenta tutte le combinazioni che si possono effettuare con i moduli per l’esercizio scritto
– tavola per il passaggio dalla Tavola I alla Tavola II
– tavola II: in questa tavola dell’addizione i riquadri sono disposti in modo che tutti i 10 risultino sulla stessa linea
– tavola per il passaggio dalla Tavola II alla tavola III
– tavola III, che si legge come la tavola pitagorica. Le due linee direttrici della cornice ricalcano la successione della serie naturale dei numeri da 0 a 9
– tavola IV
– tavola V
– tavola VI: la tombola dell’addizione.
Questa è la tavola con asticine per l’addizione:
Moduli per l’esercizio scritto
Nei moduli per l’esercizio scritto avremo sulla colonna di sinistra (primo addendo) sempre lo stesso numero (da 1 a 9), che viene sommato successivamente coi numeri da 1 a 9 (secondo addendo, nella colonna centrale). A destra si scrivono i numeri che rappresentano i totali. Dopo la stampa ritagliate i moduli lungo le linee verticali.
Questo materiale per gli esercizi scritti conduce il bambino ad impadronirsi di tutte le possibili combinazioni intorno al 10, necessarie e sufficienti da memorizzare. Stampatene tutte le copie che il bambino desidera.
Esercizi per l’addizione
Questi cartellini contengono tutte le combinazioni possibili, che rientrano nelle tavole dell’addizione, ed a parte, tutti i risultati corrispondenti:
cartelli delle operazioni
Prima tavola dell’addizione – Tavola I
Questa tavola rappresenta tutte le combinazioni che si possono effettuare con i moduli per l’esercizio scritto.
In essa ogni numero da 1 a 9 risulta addizionato con la serie dei numeri da 1 a 9.
Osservando la tavola, si vede che in ogni colonna è sempre presente un 10 come totale. Nella prima colonna (quella dell’1) il 10 è l’ultimo totale ottenuto, il penultimo nella colonna del 2, il terzultimo nella colonna del 3 ecc.. , mentre occupa la prima posizione nella colonna del 9.
Passaggio dalla tavola I alla tavola II
Il 10, nella tavola I, risulta sempre composto dall’unione di quegli stessi gruppi che il bambino ha avuto modo di conoscere fin da quando lavorava con le aste numeriche, quando, attraverso vari spostamenti, formava aste tutte di lunghezza 10 così:
9+1=10
8+2=10
7+3=10
6+4=10.
Sappiamo che 5+5=10 non è possibile con le aste numeriche per la presenza nella serie di una sola asta del 5: in realtà potremmo eseguire l’operazione 5×2, facendo ruotare l’asta di 180° gradi.
Le rimanenti combinazioni
4+6=10
3+7=10
2+8=10
1+9=10
sono semplicemente l’inverso delle combinazioni precedenti.
Disporre di aste rigide che si possono spostare per formare aste di valore 10 chiarisce il fatto che le successive combinazioni si rifanno alle precedenti e fa risaltare la differenza che esiste tra le nove combinazioni considerate nel loro complesso e la necessità di dislocare gli elementi che costituiscono le prime quattro combinazioni per poter concretizzare le ultime quattro.
Le combinazioni rappresentano il fatto più importante. Prendiamo ad esempio la combinazione 3+7=10. Se su questa combinazione si interviene con il dislocamento dei pezzi componenti cambiandoli in 7+3=10, risulta sempre la stessa combinazione, anche se sotto un altro aspetto, quasi come succede per una stessa moneta vista nel suo dritto e nel suo rovescio.
Ciò che occorre memorizzare, quindi, è la combinazione, ed ogni combinazione di gruppi diseguali di presenta doppia, dal punto di vista della posizione dei termini che la compone. Questo “duplicato inverso” può essere eliminato in una tavola semplificata, nella quale siano presenti tutte le possibili combinazioni, dove il necessario è ciò che è sufficiente:
Per il passaggio dalla Tavola I alla Tavola II nelle scuole Montessori si utilizzano oggi dei rettangoli di cartoncino che vengono utilizzati per coprire via via le combinazioni ripetute sulla Tavola I: ne risulta che la tavola si presenta suddivisa in due parti triangolari. Soltanto in quella in basso a sinistra si possono leggere le 45 combinazioni rimaste. Tuttavia, per ottenere la Tavola II, dovremo idealmente tagliare in strisce verticali le combinazioni rimaste, per riallinearle in modo che tutte le addizioni con 10 per totale si trovino sulla stessa riga.
Seconda tavola dell’addizione – Tavola II
Nella seconda tavola dell’addizione i riquadri sono disposti in modo che tutti i 10 risultino sulla stessa linea.
In questa tavola si trovano tutte le combinazioni dei gruppi che non raggiungono la decina, che si trovano al di sopra della linea in cui i risultati sono uguali a 10; tutte le combinazioni dei gruppi che superano la decina si trovano invece al di sotto della linea.
Nella Tavola II i riquadri organizzati secondo la linea del 10 offrono questo schema generale: in ogni riga sono presenti le combinazioni i cui totali risultano uguali.
Possiamo contrassegnare con colori meno accesi o con un carattere tipografico più piccolo, i duplicati delle combinazioni che è possibile eliminare alla scopo di ottenere quelle fondamentali. Le scomposizioni si verificano più volte ripetute con termini invertiti e, siccome si distinguono le ripetizioni, contrassegnandole con un colore più chiaro (ad esempio), si vede che esse vanno aumentando di numero dalla seconda colonna in avanti; vale a dire che ci si imbatte in un doppione nella colonna del 2, in due in quella del 3, ecc… e in otto nella colonna del 9.
Nella Tavola II, ogni colonna ha inizio con la combinazione in cui i due addendi sono fra loro uguali: 1+1 2+2 3+3 ecc…, e le altre combinazioni si svolgono (ma il 9+9 inizia e conclude la colonna) verso il basso.
Tutte le combinazioni della Tavola I si trovano nella Tavola II, procedendo a ritroso obliquamente e passando, in tal modo, attraverso tutte le colonne, fino alla prima.
Al di sopra della diagonale, cioè sopra la linea degli addendi uguali, si ritroverebbero le combinazioni ripetute in senso inverso (contrassegnate con colore pallido).
Se dalla Tavola I si eliminano dunque i duplicati, otteniamo una tavola semplificata contenente tutte le possibili combinazioni: questa Tavola II si può leggere e studiare come la tavola pitagorica per la moltiplicazione.
Leggendo le addizioni rimaste in ciascuna colonna, si vede che esse cominciano sempre con un numero addizionato a se stesso.
C0sì, ad esempio, considerando la colonna col 4+4:
– troviamo poi 3+4=7 (che si può leggere anche 4+3=7) nella colonna precedente e nella sua riga immediatamente superiore (salendo di una posizione in diagonale, insomma)
– nella colonna ancora più a sinistra (quella del 2) e nella riga ancora più in alto (salendo cioè in diagonale di un’altra posizione), troviamo 2+4=6 (che si può leggere anche 4+2=6).
– avvalendosi della proprietà commutativa dell’addizione, il bambino che lavora alle combinazioni del 4 troverà quelle non presenti (perchè già eliminate) rispettivamente nelle colonne del 3 del 2 e dell’1, dove il 4 è presente come secondo addendo.
La stessa cosa si osserva per tutti i numeri, procedendo obliquamente da destra a sinistra.
Per eseguire tutte le combinazioni di un dato numero partendo dalla minore, ad esempio tutte le addizioni relative al 3:
– partiamo da 1+3 della prima colonna
– proseguiamo in obliquo verso destra, di colonna in colonna, scendendo sempre di una riga: 2+3 3+3
– giunti a 3+3 si prosegue verticalmente sulla stessa colonna.
Terza tavola dell’addizione – Tavola III
Trascriviamo, uno sotto l’altro, colonna dopo colonna, i totali delle addizioni presenti nella Tavola I:
Costruiamo poi una cornice contenente la serie dei numeri da 1 a 9, prendendo lo zero per angolo. Si ottiene così questa tavola:
La Tavola III si legge come la tavola pitagorica: per esempio 8+5=13. Le due linee direttrici della cornice ricalcano la successione della serie naturale dei numeri da 0 a 9.
Lungo la diagonale si incontrano via via i doppi dei numeri presenti nella cornice, e fuori della diagonale non c’è altro che la ripetizione simmetrica delle addizioni presenti in ciascuna delle due metà. Per questo motivo basta imparare a memoria soltanto metà della tavola, cioè 45 combinazioni.
Quarta tavola dell’addizione – Tavola IV
Possiamo ridurre la Tavola III in questo modo:
– nella tavola, ogni numero da 1 a 9 si conclude, al termine delle rispettive righe, con il suo doppio.
– si vedono inoltre i numeri uguali incasellati in allineamenti ascendenti e discendenti tra loro paralleli e perpendicolari alla diagonale principale
Per poter leggere la Tavola IV si procede verso destra fino a raggiungere il doppio del numero di partenza; se il totale dell’addizione è superiore a quel doppio (e questo accade quando il secondo addendo è maggiore del primo), si scende verticalmente fino alla riga che indica il livello del secondo addendo.
Prendiamo ad esempio l’addizione 4+7:
– si procede fino al doppio del 4 (4 x 2=8)
– si scende verticalmente fino alla riga del 7: il totale è 11.
Se desideriamo addizionare 5+8, partiamo allo stesso modo dal doppio del 5 (10) e poi scendiamo verticalmente fino alla riga dell’8, e troveremo il 13.
E’ evidente che, per eseguire ad esempio la somma 8+5, per la proprietà commutativa, opereremo in maniera che il primo addendo sia quello minore, cioè il 5.
Bisogna però dire che il bambino trova molto facilmente il totale in questo modo: punta i due addendi sulla striscia verticale, sposta poi le due dita orizzontalmente verso destra finchè un dito raggiunge la diagonale che limita la tavola, e a questo punto scende verticalmente fino ad incontrare la riga orizzontale indicata dall’altro dito.
Quinta tavola dell’addizione – Tavola V
Eseguendo parecchie di queste addizioni sulla Tavola IV si osserva che i risultati incontrati lungo la diagonale principale sono sempre numeri pari, e che quelli lungo la diagonale immediatamente al di sotto e parallela sono dispari. Perciò, queste due serie di numeri bastano ad indicare ogni possibile totale di addizioni entro il 18. Possiamo quindi ridurre la Tavola IV in questo modo:
ottenendo la Tavola V.
Prendiamo come esempio l’addizione 5+8
– si procede orizzontalmente fino ad incontrare i rispettivi doppi, cioè 10 e 16
– si percorre la diagonale con direzione convergente, raggiungendo il 12 nello scendere, e il 14 nel salire
– il risultato si trova nella casella che sta tra il 12 ed il 14, sulla diagonale dei numeri dispari: 13
Prendiamo ora ad esempio l’addizione 3+7:
– arrivati al doppio 6+14 si procede in senso contrario
– sulla diagonale troviamo la casella del 10: questa volta il totale, essendo pari, si trova proprio sulla diagonale principale.
Prendiamo poi ad esempio l’addizione 3+9:
– avanziamo tra il 6 e il 18
– le dita si incontrano su un numero comune che si trova sulla diagonale: 12.
L’uso di due bastoncini per parte, che vengono opportunamente separati, dà a questo esercizio l’aspetto di gioco.
Dopo molti esercizi, il bambino potrà arrivare ad alcuni interessanti punti di coscienza:
– la somma di due numeri pari è un numero pari
– la somma di un numero pari e di un numero dispari è un numero dispari
– la somma di due numeri dispari è un numero pari.
Inoltre, la somma di due numeri è uguale alla media dei loro doppi. Infatti, intendendo per media aritmetica “la somma di due o più numeri divisa per il numero di essi” avremo ad esempio:
4+6= (4×2) + (6×2) x 1/2 = [2 x (4+6)] :2 = 10
Tavola dell’Addizione VI – Tombola dell’addizione (o Tavola con tombolini)
Oltre a queste cinque tavole di confronto, viene usata poi una sesta tavola con 81 totali mobili: è la Tombola dell’addizione.
Il tavoliere delle asticine Montessori per l’addizione – La tavola dell’addizione con le asticine serve a introdurre le addizioni oltre il dieci. Si tratta di un materiale che permette di studiare, analizzandoli nei loro particolari, i passaggi già esaminati attraverso il serpente dell’addizione.
Qui il post:
Il tavoliere delle asticine Montessori per l’addizione è una tavola suddivisa in 18 colonne e 10 righe, che formano una quadrettatura di 2 x 2 cm, nella versione originale. Una grossa linea verticale rossa situata fra la decima e l’undicesima (cioè dopo il numero 10) divide in due parti la tavola. Il materiale è completato da 9 asticine blu e nove asticine rosse, numerate entrambe da 1 a 9. Le asticine blu sono lisce, mentre quelle rosse sono quadrettate.
Le suddivisioni sono contrassegnate da numeri posti nella parte superiore che, in corrispondenza dei quadretti sottostanti, vanno da 1 a 10 alla sinistra della linea divisoria, e da 11 a 18 alla sua destra. I numeri da 1 a 10 sono scritti in rosso, mentre quelli da 11 a 18 in blu o nero. Sotto la striscia orizzontale che reca i numeri, sono presenti altre 10 strisce orizzontali: ne risulta una scacchiera rettangolare di 18 quadretti vuoti di base e di 10 di altezza.
Lo scopo del tavoliere delle asticine Montessori per l’addizione è quello di mostrare chiaramente il passaggio attraverso il 10. Accompagnano il materiale due serie di asticine di legno della stessa altezza dei quadretti e di lunghezza variabile da 1 a 9 quadretti:
– nella prima serie le asticine sono blu e non risultano suddivise in quadretti; alla fine portano il numero che corrisponde alla quantità che rappresentano
– nella seconda serie, di colore rosso, le asticine risultano suddivise in tanti quadretti quante sono le unità di ciascun gruppo da esse rappresentato. Inoltre, nell’ultimo quadretto di ogni asticina, è presente il numero corrispondente alle unità che compongono il gruppo.
Ho preparato una versione piccola del tavoliere (che sta in un foglio a4 orizzontale) e una versione un po’ più grande (occorre unire tra loro due fogli a4 per ottenere il tavoliere completo):
Oltre al tavoliere il materiale comprende tutte le tavole di controllo previste da Maria Montessori, compresa la tombola dell’addizione:
– moduli per l’esercizio scritto
– cartelli delle operazioni per le addizioni
– tavola I: questa tavola rappresenta tutte le combinazioni che si possono effettuare con i moduli per l’esercizio scritto
– tavola per il passaggio dalla Tavola I alla Tavola II
– tavola II: in questa tavola dell’addizione i riquadri sono disposti in modo che tutti i 10 risultino sulla stessa linea
– tavola per il passaggio dalla Tavola II alla tavola III
– tavola III, che si legge come la tavola pitagorica. Le due linee direttrici della cornice ricalcano la successione della serie naturale dei numeri da 0 a 9
– tavola IV
– tavola V
– tavola VI: la tombola dell’addizione.
Per utilizzare il materiale il bambino colloca sul tavoliere un’asticina blu, quella del 7 ad esempio, in alto a sinistra, subito al di sotto dei numeri;
pone poi accanto ad essa un’asticina rossa, ad esempio quella del 5.
Vede così che le due asticine insieme oltrepassano la linea rossa e arrivano al quadretto del 12, che rappresenta il totale dell’addizione considerata: 7+5=12.
L’asticina del 5 risulta a cavallo della linea rossa: 3 quadretti sulla sinistra e 2 sulla destra. Il 5 ha ceduto cioè 3 unità per completare il 10, e soltanto 2 hanno sconfinato nella seconda decina.
Esempi di addizione:
7+5=12
8+8=16
6+9=15
9+2=11
5+6=11
In questo stesso modo, si possono ripetere tutte le possibili combinazioni; ai bambini tra i 5 e i 6 anni piace molto elencare queste combinazioni una ad una.
Il tavoliere delle asticine Montessori per l’addizione, che serve ad esercitarsi sull’addizione parziale di gruppi entro la decina (serpente dell’addizione e tavoliere delle asticine), si completa con una serie di tavole di controllo per l’addizione ed esercizi scritti, che accompagnano il bambino nella memorizzazione necessaria per il calcolo veloce.
_________________________
Il tavoliere delle asticine Montessori per l’addizione
Può essere un ottimo stimolo alla lettura per bambini poco motivati, ma si rivela un gioco divertente anche come racconto per i più piccoli, che ancora non sanno leggere, e come gioco di “caccia al numero”.
Avevo ricevuto tempo fa un bellissimo racconto di pirati preparato in questo modo, da Sybille di Buntmond; qui propongo un racconto di Gnomi ed altri esseri magici, sempre alla ricerca di un tesoro.
Ho preparato le carte in varie versioni. Per le versioni con disegni da colorare ho utilizzato il materiale offerto dal sito: http://www.midisegni.it/disegni.html
Il materiale comprende:
– corsivo con disegni
– corsivo senza disegni
– stampato maiuscolo con disegni
– stampato maiuscolo senza disegni.
Il tesoro dello Gnomo Ghioffo – stampato maiuscolo con disegni
Il serpente dell’addizione è un esercizio che si può introdurre parallelamente a quello delle catene di 100
e delle catene di 1000,
e che ha lo scopo di far eseguire quasi meccanicamente piccole addizioni di unità, introducendo i bambini al calcolo mentale.
Per giocare al serpente dell’addizione occorrono semplicemente le barrette di perle colorate e quelle di perle dorate (per il 10).
Se non vuoi acquistarle, trovi il tutorial per realizzarle in proprio qui:
Se non ti è possibile, puoi anche pensare di stampare la versione virtuale, che trovi qui:
E’ necessario disporre di una certa quantità di barrette. Il numero rappresentato da ciascuna di esse si conosce contando le perle che la compongono. A poco a poco, però, il colore aiuterà a riconoscere la quantità ed eliminerà l’impegno di dover contare una perla alla volta.
Si comincia l’esercizio disponendo in riga una certa quantità di bastoncini, scegliendoli a caso. Almeno in un primo momento, però, sarà meglio disporre i bastoncini in modo tale che i bastoncini-addendi in gioco (due o più) non diano come somma oltre la decina. Questi bastoncini andranno allineati su un lungo tavolo o sul pavimento. Per fare in modo che non risulti troppo lunga, la linea non è diritta ma sinuosa, e ricorda un serpente.
Si inizia il conteggio e non appena si giunge a 10 unità, si isolano i bastoncini sommati, sostituendoli con un bastoncino dorato della decina. Quindi, a partire dalla decina, si riprende a contare fino a raggruppare altre dieci unità e, ancora, un bastoncino dorato va a sostituire quelli sommati, che si tolgono dal serpente. E così si procede fino ad esaurire il conteggio.
Assistiamo a questa trasformazione: il serpente muta pelle e diventa via via tutto d’oro , e bastoncini di uguale lunghezza vanno via via ad occupare il posto di quelli di lunghezza diversa. Il conteggio è servito a trasformare in decine quantità minori, destinate a fondersi nel dieci, base del sistema decimale.
L’esercizio offre la possibilità di eseguire semplici addizioni nel limite del dieci, dal momento che ogni volta si comincia daccapo, senza tener conto di quei bastoncini delle decine che si vanno allineando lungo il cammino. E’ un’attività sempre uniforme che va ripetendosi e che finisce col rendere facile, rapida e meccanica l’addizione di numeri inferiori al dieci.
In realtà si tratta di un grande lavoro di conteggio delle unità, che costringe a riflettere e ad eseguire un certo numero di sottrazioni contemporaneamente alle addizioni, per calcolare la quantità eccedente la decina, dopo che essa è stata formata.
Su questa particolarità si sviluppa l’esercizio con tutte le sue varietà, risultanti dai possibili accostamenti, nella formazione del serpente, di bastoncini differenti.
Poniamo il caso che il serpente cominci coi numeri 6 e 5:
la loro somma dà 11. Si isolano i due bastoncini, sostituendoli con un altro dorato, ma c’è ancora una perla (l’ultima del bastoncino marrone) che completa la quantità espressa dalla somma 5+6, cioè 5+6 è uguale a 10+1.
Questo uno appartiene al 6 che è stato isolato insieme al bastoncino del 5, infatti 6 = 5+1. Questo 1 che rimane è ancora da contare.
Proseguendo, supponiamo che gli altri bastoncini che seguono siano 8 e 6. L’addizione che si presenta per prima è 1+8=9, quindi si continua a sommare 9+6 = 15 = 10+5. Si isolano perciò i bastoncini 1, 8 e 6, sostituendoli con un bastoncino del 10 e uno del 5. Questo 5 è ciò che è rimasto del 6.
Questi resti di cui abbiamo parlato devono potersi distinguere dai bastoncini colorati che costituiscono il serpente. Questi resti rappresentano la quantità che si è dovuta mettere da parte, poichè il bastoncino colorato conteggiato solo parzialmente non può essere spezzato. Però bisogna ricordarsi di tenerne conto nell’addizione successiva. Per rappresentare questi resti, c’è un materiale complementare che elimina ogni possibile confusione: i bastoncini per i cambi:
1 – un bastoncino di 1 perla nera
2- un bastoncino di 2 perle nere
3 – un bastoncino di 3 perle nere
4 – un bastoncino di 4 perle nere
5 – un bastoncino di 5 perle nere
6 – un bastoncino di 5 perle nere e 1 bianca
7 – un bastoncino di 5 perle nere e 2 bianche
8 – un bastoncino di 5 perle nere e 3 bianche
9 – un bastoncino di 5 perle nere e 4 bianche
L’uso di nero e bianco e la loro particolare disposizione facilitano la scelta dei pezzi, che si riconoscono a prima vista.
Se non avete la possibilità di utilizzare perle vere per il gioco del serpente dell’addizione, ho preparato anche i bastoncini dei cambi in versione stampabile:
Esempi pratici
Facciamo degli esempi pratici. Componiamo questo serpente:
1 + 4 + 9 + 2 + 6 + 9 + 2 + 4 +8 + 6 + 3 + 7 + 5 + 3 + 4 +2
Il bambino comincia a contare le perle, e arrivato a 10 mette un segno a dividere la decina dal “resto”
Stacchiamo le barrette interessate al conteggio, e prendiamo la barretta della decina che abbiamo ottenuto, e la barretta del cambio relativa alla parte restante (in questo caso 1+4+9= 10 e 4):
Mettiamo da una parte la decina, ed attacchiamo al serpente la barretta nera del cambio:
Conserviamo quindi a parte le perle colorate che abbiamo tolto al serpente, e che ci serviranno per la prova:
Continuiamo il gioco addizionando la barretta del cambio al serpente, fino a raggiungere una nuova decina. Nell’esempio dovremo sommare 4 + 2 + 6
Otterremo una seconda barretta della decina, e avremo bisogno di una barretta dei cambi da 2 da attaccare al serpente:
Eliminiamo da ogni conteggio la barretta da 4 del cambio precedente:
quindi attacchiamo il nuovo cambio ottenuto (due) al serpente, e conserviamo da una parte le decine ottenute, a dall’altra le barrette colorate tolte al serpente:
Ora dunque dobbiamo sommare 2 e 9; avremo una nuova decina e un cambio da 1:
Poi avremo 1+2+4+8, ed otterremo una decina e una perla del cambio da 5:
poi 5+ 6; avremo una decina ed un resto di 1:
poi 1+3+7, ed avremo 1 decina e un cambio da 1:
poi 1+5+3+4, ottenendo una decina e un cambio di 3:
la barretta del cambio da 3 si attacca alla parte terminale del serpente, che è 2:
non arriviamo a comporre una decina nuova, quindi l’operazione si conclude conteggiando un avanzo di 5, cioè una barretta dei cambi da 5:
Eliminiamo dal conteggio il vecchio cambio (quello di 3 perle) e poniamo il cambio da 5 insieme alle decine, e la barretta del 2 insieme alle altre barrette colorate tolte via via dal serpente.
Il risultato dell’addizione 1 + 4 + 9 + 2 + 6 + 9 + 2 + 4 +8 + 6 + 3 + 7 + 5 + 3 + 4 +2 è 75:
cioè 10 10 10 10 10 10 10 10 5. Ma come possiamo sapere se è corretto? Basterà contare tutte le perle colorate che formavano il serpente in origine, sempre raggruppando tra loro le barrette a formare decine colorate. Se ci occorre spezzettare le barrette, potremo sostituirle con un equivalente di perle nere dei cambi. Nel nostro esempio dovremo sostituire la barretta dei due con due barrette da uno:
ed avremo:
9+1=10, 9+1=10, 8+2=10, 7+3=10, 6+4=10, 6+4=10, 5+4+1=10, e 3+2=5; cioè 10 10 10 10 10 10 10 10 5
l’operazione è corretta. Il risultato è 75.
Torniamo ora all’immagine del serpente già presentato più sopra:
L’immagine rappresenta i cambi avvenuti per formare le decine. Le quantità originarie incolonnate a sinistra sono state via via sostituite, dando luogo alla disposizione rappresentata nella linea di perle a destra. Fra le due disposizioni possiamo vedere ciò che rimaneva dei bastoncini che nel corso dell’operazione risultavano eccedere la decina: resti che vennero via via sommati con i bastoncini che li seguivano. Il risultato del serpente è 62, ossia: 10 10 10 10 10 10 2
A volte i bambini costruiscono un serpente molto lungo, che assomma a molte centinaia. A esercizio concluso, si contano i bastoncini delle decine disponendoli uno accanto all’altro, verticalmente: appena riuniti 10 bastoncini, si sostituiscono con un quadrato del centinaio, e così si prosegue coi cambi, fino alla fine. Il totale risalta facilmente, proprio per la differente forma dei risultanti gruppi del sistema decimale ( quadrato per le centinaia, linea per la decina, punto per le unità).
La verifica dell’operazione eseguita si effettua raccogliendo tutti i bastoncini via via usciti dal gioco e riunendoli a due a due (se possibile), in modo che ogni coppia costituisca una decina. Nel caso del serpente 5 6 8 6 2 5 1 4 9 3 4 7 9 si raggrupperanno così:
9+ 1
8+2
7+3
6+4
6+4
5+5
9
e si verificherà che ogni gruppo possa sostituirsi con una decina del risultato. In questo caso c’è perfetta corrispondenza:
L’esercizio del serpente fissa l’attenzione del bambino sulla difficoltà di contare per dieci. Questa difficoltà, ripetendosi costantemente, porta il bambino a procedere in modo esatto, dal momento che non lo preoccupa la serie di decine che via via si lascia indietro.
Nei metodi comuni, quando si addizionano gruppi di unità che formano più decine, questo accumulo gravoso e molesto si trascina, rendendo faticoso l’andare avanti. Invece la difficoltà di calcolo è unica ed è sempre la stessa, per quanto grande sia l’ampiezza dei conti da eseguire, e risiede in quel salto attraverso il 10 che presuppone un’attività mentale, esige cioè piccole addizioni e sottrazioni per arrivare a completare le decine, e il calcolo dei resti che devono essere aggiunti ai gruppi successivi.
Gli esercizi col serpente, ripetuti per lungo tempo, finiscono per rendere meccanico il lavoro della mente intorno al 10: a poco a poco sparisce la lenta attività di ragionamento, e si sostituisce con un meccanismo mentale. Le leggi che regolano le attività razionali affidano al deposito della memoria le conoscenze acquisite, per fare in modo che ci siano sempre energie disponibili da dedicare a lavori successivi. Questo deposito della memoria è un grande tesoro che permette di avanzare.
Si tratta della teoria montessoriana del “valore del subconscio”. Secondo la Montessori il subconscio è deposito e riserva di impressioni assorbite e di conoscenze acquisite. Il subconscio è paragonabile a una grande stanza buia nella quale sono immagazzinate le esperienze attraverso cui l’individuo è passato nel corso della sua vita. La stanza non è arredata: i mobili non vi sono disposti con una funzione, ma sono ammassati come in un magazzino. La mente che cerca una soluzione è simile a una torcia nelle mani di un ladro che sceglie la cosa per lui più preziosa in quel momento. Il fascio di luce si arresta: ha trovato quello che cercava, e questo cercare e trovare è ciò che chiamiamo “portare alla luce della coscienza”.
Le nuove acquisizioni, poi, devono prima essere filtrate dal ragionamento, e non si dirigono mai direttamente alla memoria ed ai suoi meccanismi.
Così, quando il bambino ha raggiunto un certo grado di maturità meccanica nel calcolo relativo ai passaggi attraverso il 10, i gruppi di decine già accumulati e lasciati indietro potranno venir trasportati di volta in volta nel posto che compete loro attraverso la memoria, grazie a passaggi che in sè non presentano ormai nessuna difficoltà.
Nell’esercizio del serpente, i due diversi lavori risultano separati, e questo permette un procedere rapido e senza fatica, consentendo il raggiungimento di risultati apprezzabili. Le decine che si accumulano si contano a parte, in una seconda fase, e i bambini lo fanno con grande piacere, provando la soddisfazione di chi si rende conto della propria ricchezza dopo aver fatto la fatica di “risparmiarla”.
Catene di perle Montessori TUTORIAL E DOWNLOAD.
Le catene di perle sono serie di barrette (di perle colorate per i numeri da 1 a 9) e di perle dorate per la decina, che rappresentano in forma lineare il quadrato ed il cubo di ogni numero. Coi bambini più piccoli si prestano ad esercizi legati al contare ed all’esplorazione del numero e del sistema decimale, coi più grandi supporta lo studio delle potenze e dell’algebra.
Qui trovi qualche suggerimento per la costruzione in proprio del materiale, o in alternativa la versione stampabile.
Catene di perle Montessori TUTORIAL E DOWNLOAD
Partiamo dalla costruzione della catena del 100 e delle altre catene del quadrato dei numeri.
Questa è la catena del 100, cioè del quadrato di 10 (da realizzare naturalmente con le perle dorate)
Se desiderate realizzare il materiale con perle vere, dopo aver preparato le 10 barrette da dieci perle, congiungetele tra loro preparando degli anellini di fil di ferro:
Se non avete la possibilità di realizzare il materiale con perle vere, potete considerare l’idea di stampare e comporre sempre con anellini di fil di ferro o graffette queste catene pronte per la stampa:
Sia che usiate perle vere, sia che vogliate ricorrere alla versione stampabile, completano il materiale le frecce per contare (blu per le decine, rosse per le centinaia):
Catene di perle Montessori TUTORIAL E DOWNLOAD
Le altre catene dei quadrati, oltre a quella del 100 (quadrato del 10) si preparano allo stesso modo, utilizzando le barrette di perle colorate
per i numeri da 2 a 9 (il quadrato di 1 è 1), congiungendo attraverso gli anellini di fil di ferro (o le graffette):
– 2 barrette del 2
– 3 barrette del 3
– 4 barrette del 4
– 5 barrette del 5
– 6 barrette del 6
– 7 barrette del 7
– 8 barrette dell’8
– 9 barrette del 9
è un materiale che, una volta preparato, si presta poi ad essere utilizzato anche per giochi con le tabelline e successivamente allo studio delle potenze dei numeri.
Questa è, se può essere utile, la versione stampabile:
E anche in questo caso, completano il materiale le frecce per contare.
Ho preparato una versione colorata (nei colori utilizzati per preparare il materiale stampabile) e una versione bianco e nero se utilizzate barrette di colori diversi (da colorare o da stampare su fogli colorati):
Catene di perle Montessori TUTORIAL E DOWNLOAD
La catena del 1000 e le altre catene dei cubi dei numeri
Per la catena del 1000, dopo aver preparato le 10 catene del 100 necessarie, congiungetele tra loro con un ulteriore anellino, in modo tale che la catena presenti un anello a congiungere le decine tra loro, e due anelli a congiungere tra loro le centinaia.
Allo stesso modo potete congiungere tra loro, se preferite, il materiale stampabile proposto più sopra, insieme alla catena del 100.
Sia che usiate perle vere sia che usiate il materiale stampabile, completano il materiale le frecce per contare.
Catene di perle Montessori TUTORIAL E DOWNLOAD
Per i cubi dei numeri da 1 a 9 congiungete tra loro:
– 4 barrette del 2
– 9 barrette del 3
– 16 barrette del 4
– 25 barrette del 5
– 36 barrette del 6
– 49 barrette del 7
– 64 barrette dell’8
– 81 barrette del 9
Questo è il materiale in versione stampabile:
Anche in questo caso, il materiale è completato dalle frecce per contare, compreso nelle frecce per contare le catene delle potenze:
Catene di perle Montessori TUTORIAL E DOWNLOAD
Versione stampabile delle perle dorate Montessori – Questo è il materiale delle perle dorate:
potete trovare il tutorial per realizzarlo in proprio qui
Versione stampabile delle perle dorate Montessori
Soprattutto pensando alle insegnanti che sentono quanto la psicoartimetica Montessori potrebbe essere d’aiuto nella scuola, non solo per il sostegno, ho anche preparato del materiale “virtuale” stampabile:
Versione stampabile delle perle dorate Montessori
Dopo aver stampato, consiglio di plastificare, o almeno di incollare ad un cartoncino per rendere il materiale più resistente e facile da maneggiare.
Potete utilizzare le barrette semplicemente ritagliate, ma sarebbe meglio completarle inserendo alle due estremità di ogni barretta una graffetta:
o un anellino di fil di ferro (basta attorcigliarlo attorno alla pinza e tagliare):
Questo accorgimento vi permetterà poi di utilizzare il materiale anche per altri giochi ed attività interessanti come il serpente dell’addizione e le catene di 100 e di 1000.
Versione stampabile delle perle dorate Montessori
Perle colorate Montessori – download. Queste sono le barrette di perle colorate Montessori:
Trovi il tutorial per realizzarle qui:
Soprattutto pensando alle insegnanti che sentono quanto la psicoaritmetica Montessori potrebbe essere d’aiuto nella scuola, non solo per il sostegno, ho anche preparato del materiale “virtuale” stampabile:
Dopo aver stampato, consiglio di plastificare, o almeno di incollare ad un cartoncino per rendere il materiale più resistente e facile da maneggiare.
Potete utilizzare le barrette semplicemente ritagliate,
ma sarebbe meglio completarle inserendo alle due estremità di ogni barretta una graffetta:
o un anellino di fil di ferro (basta attorcigliarlo attorno alla pinza e tagliare):
Questo accorgimento vi permetterà poi di utilizzare il materiale anche per altri giochi ed attività interessanti come il serpente dell’addizione…
_________________________________
Numeri e gettoni Montessori – come costruire il gioco in proprio. Dopo il casellario dei fuselli
e le aste numeriche
abbiamo un terzo materiale, che consiste in dieci cartoncini separati, su ciascuno dei quali è scritto un numero: 1 2 3 4 5 6 7 8 9 10, e 55 piccoli oggetti separati che possono essere gettoni colorati, giocattolini uguali, palline, monetine, tappi delle bottiglie di plastica, ecc…
Trovi le indicazioni per la presentazione del materiale e gli esercizi qui:
Se può essere utile, ho preparato due giochi in formato pdf, stampabili:
la versione a colori
Se scegliete la versione in bianco e nero, basterà stampare su carta colorata (rossa o arancione):
Dopo aver stampato la versione che preferite, consiglio di incollare i fogli a del cartone, anche di recupero:
ed eventualmente di plastificare:
prima di procedere al ritaglio:
E il vostro gioco dei Numeri e gettoni Montessori è pronto:
_________________________________
Numeri e gettoni Montessori
Aste numeriche Montessori – SOMME DI PROGRESSIONI ARITMETICHE. Come già accennato qui
coi ragazzi più grandi, nello studio dell’algebra, possiamo tornare ad utilizzare un materiale che hanno conosciuto quando avevano circa 4 anni: le aste numeriche.
Se non disponete del materiale, potete utilizzare queste aste da stampare, plastificare e ritagliare.
Al livello della Casa dei Bambini, si disponevano le aste di lunghezza graduale una sotto l’altra, in modo che risaltassero le diverse lunghezze e i loro rapporti.
Poi, uno degli esercizi consisteva nel collocare l’asta più corta a fianco della penultima, poi l’asta del 2 accanto all’asta dell’8, l’asta del 7 accanto all’asta del 3 ecc… in modo da ottenere aste uguali a quella del 10. Solo l’asta del 5 non aveva compagno, indicando perciò la metà di 10.
In questo modo si ottenevano cinque aste di valore 10 e una di valore 5: il conteggio di tutte le unità contenute nelle aste era così facilitato dalla loro stessa disposizione, che rappresentava la moltiplicazione 10×5=50 e l’addizione 50+5=55
Lo stesso concetto può essere rappresentato su carta quadrettata, in questo modo:
ottenendo un quadrato che misura 10×10 (10²).
Disponendo poi i segmenti in questo modo:
si arriva ad occupare metà del quadrato iniziale, ottenendo 5 righe di valore 10 l’una sull’altra, cioè 10²/2, ma avanza una mezza riga, un valore 5 ossia 10/2.
Considerando il 10 come maggior numero raggiunto nella serie naturale data dalle aste, si deduce che la somma della serie naturale dei numeri è uguale alla metà del quadrato di 10 + la metà di 10
1+2+3+4+5+6+7+8+9+10 =
= 10²/2 + 10/2 =
= (10²+1o)/2 =
= (100+10)/2=
=110/2 = 55
La stessa cosa di verificherà procedendo oltre al 10, collocando sempre l’1 vicino alla penultima quantità che differisce dalla maggiore per una unità e così via per le altre. Questo è ad esempi quello che succede prendendo in considerazione il numero 16:
16²/2 + 16/2
da cui
1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16 = (16² + 16):2 = (256+16):2 = 272:2 = 136
Questo procedimento risulta molto più semplice che non addizionare un numero dopo l’altro, e la disposizione geometrica facilita moltissimo.
Se si dovessero addizionare i numeri da 1 a 100, la semplificazione sarebbe ancora più evidente. Invece di eseguire l’addizione:
1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19+20+21+22+23+24+25
+26+27+28+29+30+31+32+33+34+35+36+37+38+39+40+41+42+43+44+45+46
+47+48+49+50+51+52+53+54+55+56+57+58+59+60+61+62+63+64+65+66+67
+68+69+70+71+72+73+74+75+76+77+78+79+80+81+82+83+84+85+86+87+88
+89+90+91+92+93+94+95+96+97+98+99+100=
basta procedere con questo semplice calcolo:
100²/2 + 100/2 = 10000/2 + 1oo/2 = 5000+50 = 5050
Questa semplificazione può essere applicata a qualsiasi grande numero, solo il calcolo può diventare più laborioso.
Per dare perciò a questo procedimento un carattere generale, che può essere applicato ad ogni addizione di numeri disposti secondo la serie naturale, si usa la lettera n (numero): è l’ultimo numero della serie. Abbiamo così la seguente formula:
1+2+3+…+n = (n² + n) : 2
Se vogliamo che i ragazzi arrivino con entusiasmo ad una formula algebrica, dice Maria Montessori, non dobbiamo spiegargliela, nè cercare di attirare la sua attenzione su di essa: conviene invece non insistere. Può essere necessario ripetere quello stesso esercizio cui si dedicava quando aveva 4 anni: lo spostamento delle aste; ripetere queste esperienze col disegno, con le liste, ecc… In questo modo, improvvisamente, l’idea prende forma e la formula che la esprime non solo apparirà interessante, ma anche necessaria, come è indispensabile il linguaggio per esprimere le idee e comunicare.
L’algebra che ricorre all’alfabeto è, con le sue formule, il linguaggio delle idee matematiche.
Quando i ragazzi arrivano a comprenderne il significato, si sviluppa in loro la tendenza a cercare, fra le esperienze fatte, idee che possano esprimersi mediante formule algebriche.
Scala marrone e torre rosa: estensioni – I set della torre rosa e della scala marrone possono essere usati insieme per creare costruzioni sia verticali sia orizzontali. I bambini possono essere lasciati liberi di sperimentare, oppure si possono seguire ad esempio questi modelli.
Le figure che si creano sono molto belle, e alcune non sono affatto semplici da realizzare…
Qui puoi scaricare le schede in formato pdf da utilizzare coi bambini per copiare gli schemi (quattro immagini per foglio, da ritagliare e plastificare). Conservate in una scatolina vicino al materiale, i bambini possono sceglierle liberamente per il loro lavoro individuale :
___________________
I spy Halloween – si tratta di un gioco sensoriale che stimola la capacità visiva e l’attenzione, adatto anche ai bambini più piccoli, semplice ed economico da realizzare.
I spy Halloween – materiale occorrente per la VERSIONE 1
– cartone (io ho usato un contenitore per pizza)
– pannolenci (o altro tessuto)
– riso
– plastica trasparente (io ho usato un ritaglio di un sacco da spazzatura)
– colla a caldo
– forbici e taglierino
– l’ideale sarebbe avere a disposizione piccoli oggettini tridimensionali, ma in alternativa si possono usare anche delle immagini a tema, come ho fatto io
– carta per preparare le schede da allegare (se volete) al gioco
I spy Halloween – come si fa – VERSIONE 1
Ritagliate due forme identiche nel cartone:
In una delle due incidete l’interno, in modo tale che rimanga soltanto una cornice, e preparate anche delle striscioline:
Incollate vari strati di striscioline intorno alla forma di cartone, per creare un certo spessore:
Foderate l’interno e la cornice col pannolenci, fissandolo sempre con la colla a caldo:
Incollate un pezzo di pannolenci anche alla cornice:
Poi incidete la parte centrale lasciando un margine che, rigirato, possa bastare a rivestire il cartone lungo lo spessore e l’altro lato della cornice:
Sul rovescio della cornice incollate la plastica trasparente:
Riempite di riso il primo cartone preparato, aggiungete gli elementi che il bambino si divertirà poi a cercare e chiudete sovrapponendo il secondo elemento (quello con la plastica), quindi chiudete con la colla a caldo:
Rivestite il retro con altro pannolenci:
Girate sul davanti e rifinite i bordi con la colla a caldo:
O se preferite con ago e filo:
I spy Halloween – materiale occorrente per la VERSIONE 2
– riso
– colla a caldo
– pannolenci
– elementi da inserire a tema Halloween
– una custodia da cd
I spy Halloween – come si fa – VERSIONE 2
Smontate la custodia, eliminate la parte centrale e rimontate (rimangono dei fori e un’apertura a lato, che chiuderemo poi col pannolenci):
Se utilizzate immagini e non elementi tridimensionali, incollateli su del cartoncino da una parte e dall’altra; il mio cartoncino aveva una facciata verde e una rossa:
Mettete nella custodia del cd del riso e gli elementi scelti:
Chiudete con del pannolenci fissato con la colla a caldo lungo i quattro lati:
I spy Halloween – il gioco può essere utilizzato così, soprattutto per i più piccoli, oppure può essere accompagnato da un elenco (illustrato o scritto),
o anche da carte (simili alle carte delle nomenclature Montessori) che possono contenere solo l’immagine,
oppure anche il nome (se il bambino sa già leggere):
Potete anche pensare di utilizzare il gioco per aiutare la memorizzazione dei nomi in Inglese:
Questo è il materiale che ho utilizzato io (immagini, carte scritte in Italiano, carte scritte in Inglese) disponibile per gli abbonati
Questo articolo fa parte dell’Album di Vita pratica:
Dinosauri – nomenclature Montessori. Sul tema dinosauri ho preparato queste carte delle nomenclature che includono le carte illustrate, i cartellini dei nomi, le carte con immagine e nome del dinosauro, e anche delle schede illustrate abbinate a schede con testo descrittivo.
Altro materiale didattico sull’argomento dinosauri si trova qui:
Dinosauri: carte delle nomenclature mute e cartellini dei nomi
Carte dei dinosauri con nomi
Dinosauri: carte illustrate e testo
disponibili per la stampa e il download qui:
queste carte delle nomenclature includono:
– le carte illustrate,
– i cartellini dei nomi,
– le carte con immagine e nome del dinosauro,
– le schede illustrate abbinate a schede con testo descrittivo.
Metodo Montessori: schede delle nomenclature per le difficoltà ortografiche – CI. Esistono molte possibilità per favorire gli esercizi di autodettatura, una volta che il bambino è avviato alla scrittura ed alla lettura; una di queste possibilità può essere quella di preparargli delle schede illustrate (nomenclature Montessori), che possono anche fornire un aiuto all’arricchimento del lessico.
Classicamente le schede delle nomenclature Montessori, a questo secondo scopo, sono organizzate per aree tematiche (animali domestici, casa, abbigliamento, mezzi di trasporto, ecc…).
In questa serie di schede propongo una classificazione diversa, in funzione dell’apprendimento delle varie difficoltà ortografiche presenti nella nostra lingua: dopo le nomenclature Montessori per le consonanti doppie
e il suono CHI,
passiamo alle parole che contengono CI (ci, cia, cie, cio, ciu).
Questa è una selezione di parole italiane che presentano appunto il suono “ci”, con diversi gradi di difficoltà; non tutte si prestano ad essere illustrate, e le parole presenti nelle schede delle nomenclature sono in grassetto. Può essere utile per preparare altri esercizi, comporre frasi, dettati, ecc…
parole di 3 lettere: ciò, cip
parole di 4 lettere: Ciad, ciao, Cile, cime, Cina, cioè, Ciro, noci
parole di 5 lettere: ciano, cicca, ciclo, cieco, cielo, cifre, cigno, cinta, cippo, Cipro, circa, Circe, circo, cirro, ciste, città, ciuco, cacio, Licia, Lucia, Lucio, micio, socio, amici, dieci, fauci, greci, acido, acini
parole di 6 lettere: cialde, ciance, cicala, ciccia, cicuta, cifosi, ciglia, ciglio, cileno, cimice, cincia, cinema, cinese, cinico, cinque, Cinzia, ciocco, cipria, ciripà, citare, citato, ciuffo, ciurma, civico, civile, accisa, bacino, cucina, cucire, cucito, decina, deciso, docile, facile, fucile, fucine, inciso, lecito, lucido, macina, nocino, nocivo, reciso, recita, ricino, tacito, Ticino, ucciso, uscire, uscito, vicino, dodici, indici, manici, medici, monaci, musici, sedici, undici,
parole di 7 lettere: cianosi, cianuro, cibarie, ciclico, ciclone, ciclope, cicogna, cicoria, cifrare, cifrato, cigolio, cilecca, Cilento, Cimabue, cimelio, cinghia, cingolo, cinismo, cintato, cintura, ciotola, cipolla, cirrosi, cisposo, cistico, cistite, citrato, citrico, ciuccio, civetta, civiltà, acidità, acidosi, acidulo, accidia, acciuga, arciere, arcigno, baciare, bacillo, Cecilia, decibel, deciduo, eccidio, forbici, incinta, incipit, Luciano, Lucilla, macigno, paciere, recinto, Sicilia, sociale, società, boccino, calcina, coccige, concime, conciso, faccino, fiocina, glicine, glucide, laicità, mancino, marcire, narciso, omicida, opacità, ovocita, piccino, placido, porcile, porcini, precise, Puccini, pulcino, rancido, sancire, scucire, scucito, siccità, suicida, unicità, vaccino, vescica, vincita, viscido, arancia, arancio, audacia, breccia, Brescia, broncio, camicia, caucciù, deficit, Fenicia, ferocia, fiducia, floscio, Francia, freccia, gruccia, guancia, guercio, omaccio, plancia, quercia, sagacia, sconcio, sfalcio, sudicio, tenacia, treccia, spinaci,
parole di 8 lettere: ciabatte, ciaccona, ciarlare, ciarpame, ciascuno, cicalare, cicalino, ciccioli, cicciona, cicerone, cicisbeo, ciclismo, ciclista, cifrario, cigolare, ciliegio, cilindro, cimitero, cincillà, cineasta, cinefilo, cinerino, cinetico, ciniglia, cinofilo, cinquina, ciottolo, cipiglio, cipresso, circense, circuire, cisterna, citofono, citosina, citrullo, equivoci, massicci, organici, pacifici, plastici, pubblici, quindici, tirabaci, alopecia, alticcio, astuccio, bisaccia, catorcio, chioccia, edificio, erbaccia, farmacia, feticcio, focaccia, fradicio, galoscia, legaccio, libecio, mendacia, meticcio, opificio, robaccia, romancia, unticcio, vitaccia, viticcio, arancino, atrocità, basicità, braccino, caducità, camicina, capacità, comicità, erbicida, eroicità, felicità, fisicità, flaccido, illecito, indeciso, leoncino, liricità, logicità, lumicino, medicine, officina, ossicino, principe, rapacità, ricucire, riuscire, tenacità, tipicità, tonicità, topicida, toracico, tubicino, velocità, veracità, vivacità, voracità, amicizia, asociale, berciare, bocciare, bocciolo, braciere, braciola, briciole, bruciare, bruciato, bruciore, cacciare, cacciato, calciare, calciato, carciofo, cencioso, ciccione, cocciuto, conciare, conciato, crociato, crociera, cruciale, cucciolo, facciata, falciare, giacinto, glaciale, gracidio, lanciare, lasciare, lerciume, lisciare, lucciola, manciata, marciare, marciume, moccioso, nocciole, omicidio, panciera, picciolo, piccione, precipuo, procinto, procione, pulcioso, ricciolo, ricciuto, roccioso, selciato, sfociare, speciale, suicidio, tacciare, triciclo, bicipite, caciotta, cucinare, cucitura, decidere, decimare, decisivo, diciotto, docilità, facilità, incidere, incisivo, incisore, lecitina, lucidare, macinare, macinato, macinino, recidere, recidivo, recitare, tacitare, uccidere, vicinato,
parole di 9: cialtrone, ciambella, cianciare, cianotico, ciarliero, cicatrice, cicerchia, ciclabile, ciclamino, ciclicità, ciclopico, ciliegina, ciminiera, cineforum, cinepresa, cinghiale, cingolato, cinquanta, cinturino, cinturone, circolare, cirillico, citazione, citologia, cittadino, ciuffetto, acrostici, antipulci, avaraccio, babbuccia, bamboccio, barcaccia, beccaccia, beccuccio, bertuccia, boccaccia, boccuccia, borraccia, cagnaccio, calduccio, cannuccia, cantuccio, cappuccio, capriccio, cartaccia, cartoccio, cartuccia, corteccia, crepaccio, dispaccio, donnaccia, efficacia, fantoccio, fattaccio, fettuccia, lanificio, lettuccio, malconcio, maleficio, massiccio, molliccio, panificio, efficacia, fantoccio, fattaccio, fettuccia, lanificio, lettuccio, malconcio, maleficio, massiccio, molliccio, panificio, pellaccia, pelliccia, polpaccio, provincia, rossiccio, salciccia, spilorcio, tempaccio, terriccio, tettuccio, traliccio, umidiccio, acaricida, addolcire, addolcito, antracite, bollicine, coroncina, corpicino, cronicità, cuoricino, difficile, esplicite, filoncino, forbicina, fungicida, germicida, indeciso, impreciso, latticini, libricino, loquacità, partecipe, pesticida, Pollicino, porticina, posticino, praticità, precocità, risarcire, ritmicità, rivincita, vagoncino, aranciata, arancione, associare, associato, bracciolo, crescione, cresciuto, crucciato, enunciato, esercizio, esorcismo, fiducioso, guanciale, imbecille, motociclo, municipio, musicisti, sbocciare, sbocciato, sbucciare, sbucciato, scacciare, scacciato, scalciare, scalciato, scocciare, scocciato, sfacciato, sganciare, sganciato, slacciare, slanciato, slacciato, spicciole, sporcizia, spulciare, sudiciume, tirocinio, tracciare, tracciato, tranciato, ufficiale, concimare, concimato, concitato, diecimila, dolciario, fanciullo, giaciglio, luccicare, panciolle, panciotto, vaccinare, vaccinato, vincitore, accidente, baciamano, bacinella, cucitrice, decisione, incidente, incidenza, incisione, occidente, oscillare, pacifista, recintato, socialità, socievole, sociologo, taciturno, uncinetto, vacillare, vicinanza,
parole di 10 lettere: ciabattare, ciabattino, ciabattona, ciarlatano, cicaleccio, ciclistico, cilindrata, cilindrico, cinguettio, cinquemila, cioccolato, ciondolare, circadiano, circolando, circonciso, circondare, circondato, citofonare, citoplasma, cittadella, civetteria, civettuolo, acciaccato, acciaieria, accigliato, acciuffato, arcipelago, bicicletta, diciannove, facilitare, inciampare, incipriare, incisività, lucidatura, racimolare, recinzione, recipiente, bocciatura, bruciatore, bruciatura, cacciavite, calciatore, coccinella, cruciverba, cucciolata, cuscinetto, falciatura, giacimento, gocciolare, gocciolina, gocciolone, lanciatore, marciatore, piccionaia, precipizio, precisione, Pulcinella, ricciolino, riccioluto, rocciatore, specialità, torcicollo, truciolato, anticipare, avvicinare, efficiente, efficienza, esercitare, medicinale, principale, principato, accasciare, accasciato, acconciare, acconciato, accorciare, accorciato, agganciare, agganciato, allacciare, allacciato, annunciare, annunciato, arricciare, arricciato, asticciola, chiocciola, cominciare, cominciato, cornicione, denunciare, denunciato, dissociare, dissociato, farmacista, forbiciata, ghiacciaia, ghiacciaio, ghiacciato, ghiacciolo, impacciato, limaccioso, minacciare, minacciato, minaccioso, misticismo, muricciolo, participio, patrocinio, pernicioso, ricacciare, ricacciato, rilanciare, rilanciato, rinunciare, scamiciato, scricciolo, setacciare, setacciato, sfiduciato, sfrecciare, turacciolo, verniciare, verniciato, balconcino, barboncino, bastoncino, beccaccino, bocconcino, bottoncino, camioncino, cappuccino, carboncino, cartoncino, complicità, cordoncino, dinamicità, elasticità, fettuccina, flaconcino, furgoncino, incapacità, infelicità, marroncino, mattoncino, palloncini, pasticcino, portoncino, pubblicità, semplicità, spadaccino, affaraccio, bestiaccia, canovaccio, casereccio, figuraccia, lavoraccio, levataccia, linguaccia, maglificio, malaticcio, pagliaccio, sacrificio, sudaticcio, superficie, centodieci, metafisici, pannolenci, pronostici,
parole di 11 lettere: ciambellano, cibernetico, ciberspazio, ciclomotore, cilindrasse, cineamatore, cinguettare, cinquantina, cinquecento, circolarità, circondario, circospetto, circostante, circostanza, cirrocumulo, cirrostrato, cistercense, cistifellea, civilizzato,
parole di 12 lettere: cialtroneria, cicatrizzare, cicatrizzato, cicciottello, cinciallegra, cincischiare, cinquantatré, cinquantenne, cioccolatini, circolazione, circonflesso, circoscritto, cittadinanza
parole di 13 lettere: cianfrusaglia, cinquantamila, cinquantennio, cinquantesimo, circonferenza, circoscrivere, circospezione, citrullaggine, Civitavecchia
parole di 14 lettere: cinematografia, cinquecentesco, circonvenzione, circoscrizione, circostanziare, circostanziato, circumnavigare, circumnavigato, civilizzazione,
parole di 15 lettere: cicatrizzazione, cinematografico, cinquecentesimo, cinquecentomila.
E queste sono le schede a colori, pronte per il download e la stampa per gli abbonati:
Il materiale comprende:
Carte mute (solo immagini)
Cartellini in stampato minuscolo
Cartellini in corsivo
Nomenclature in stampato minuscolo
Nomenclature in corsivo
Carte mute (solo immagini)
____________________
Cartellini in stampato minuscolo
____________________
Cartellini in corsivo
_____________________
Nomenclature in stampato minuscolo
_____________________
Nomenclature in corsivo
______________________
Qui puoi trovare tutti i dettati ortografici pubblicati e classificati per tema e per difficoltà ortografica: https://www.lapappadolce.net/
Tutte le schede delle nomenclature finora pubblicate si trovano qui:
https://www.lapappadolce.net/category/download/materiale-didattico/download-carte-montessori/
________________________________________
Nomenclature Montessori per le difficoltà ortografiche: parole con CHI. Come già detto per le schede delle nomenclature per parole di tre lettere
e per le schede delle nomeclature per parole di quattro lettere,
una volta che il bambino ha fatto molti esercizi di composizione di parole per dettatura con l’alfabeto mobile, è pronto per gli esercizi di autodettatura, cioè per comporre autonomamente parole che egli stesso ha pensato, senza averle sentite dalla voce di altri.
Esistono molte possibilità per favorire questo genere di esercizio, una può essere quella di preparare delle schede illustrate, che possono anche fornire un aiuto all’arricchimento del lessico.
Classicamente le schede delle nomenclature, a questo secondo scopo, sono organizzate per aree tematiche (animali domestici, casa, abbigliamento, mezzi di trasporto, ecc…).
Qui propongo una classificazione diversa, in funzione dell’apprendimento delle varie difficoltà ortografiche presenti nella nostra lingua: dopo le consonanti doppie,
passiamo al suono CHI.
Questa è una selezione di parole italiane che presentano appunto il suono “chi”, con diversi gradi di difficoltà; non tutte si prestano ad essere illustrate e le parole presenti nelle schede delle nomenclature sono in grassetto:
Parole di 5 lettere: buchi, cachi, chilo, chimo, china, duchi, pochi.
Parole di 6 lettere: banchi, chiave, chiesa, chiodo, chioma, chiosa, chissà, chiuso, occhio, schiva, fuochi, cuochi, giochi.
Parole di 7 lettere: borchia, cerchio, chiasso, chiatta, chiazza, chicchi, chiglia, chimera, chimica, chinare, chinato, chiosco, cocchio, fachiro, foschia, macchia, maschio, mischie, mucchio, muschio, nicchie, pacchia, picchio, racchia, schiavo, schiena, schiera, schiuma, schiuso, secchio, teschio, tirchio, tronchi, vecchio, vischio.
Parole di 8 lettere: achillea, alchimia, anarchia, arachide, becchime, becchino, bocchino, boschivo, branchia, cecchino, chiamare, chiamato, chiarire, chiarito, chiarore, chiedere, chinotto, chioccia, chiostro, chirurgo, chitarra, chiudere, chiunque, chiusero, chiusino, chiusino, chiusura, colchico, crocchio, facchino, gerarchi, giochini, granchio, macchine, maschile, meschino, monarchi, moschino, occhiaia, occhiali, occhiata, orchidea, orecchio, panchina, psichico, schiappa, schietto, schifare, schifare, schifoso, schioppo, schivare, schivato, spicchio, specchio, spocchia, tacchino, turchino, vichingo, zecchino, zucchine.
Parole di 9 lettere: anarchico, antichità, bacchiare, batocchio, bicchiere, birichino, bronchite, brulichio, capocchia, cavicchio, cerchiare, cerchiato, cerchione, chiarezza, chiarirsi, chiassoso, chiavetta, chiazzato, chicchera, chiedendo, chiedersi, chiesetta, chimerico, chirurgia, cicerchia, cocchiere, conocchia, coperchio, cotechino, cucchiaio, dischiuso, eschimese, finocchio, fischiare, fuochista, gerarchia, ginocchia, ginocchio, inchiesta, inchinato, luccichio, malocchio, manichino, marchiare, marchiato, microchip, mischiare, mischiato, monarchia, muschiato, nocchiero, occhiello, occhietto, orecchini, ossibuchi, pacchiano, parecchio, pechinese, picchiare, picchiato, pidocchio, Pinocchio, pistacchi, racchiuso, rachitico, radicchio, ranocchio, raschiare, raschiato, rinchiuso, rischiare, rischioso, sarchiare, sarchiato, schiarire, schiavitù, schienale, schierare, schierato, schifezza, schiodare, schiodato, schiudere, schiumare, schiumoso, schizzare, schizzato, secchiata, secchiona, socchiuso, stecchini, stecchire, stecchito, succhiare, succhiato, tarchiato, torchiare, torchiato, vecchiaia, vecchiume, vischioso.
Parole di 10 lettere: adocchiare, adocchiato, alchimista, archibugio, architetto, architrave, archiviare, archiviato, archivista, Arlecchino, arricchire, arricchito, attecchire, attecchito, autarchia, autarchico, baracchino, catechismo, cerchietto, chilometro, chiocciola, conchiglia, cornacchia, crocicchio, cucchiaino, dichiarare, dichiarato, fischiando, formichina, franchigia, giradischi, gracchiare, inchiodare, lenticchie, macchiette, macchinoso, marmocchio, occhialuto, occhiatina, occhiolino, pachiderma, pannocchia, parrocchia, pennacchio, pernacchia, picchiando, richiamare, richiamato, richiedere, richiudere, rischiando, schiantato, schiarirsi, schioccare, schiudersi, secchiello, semichiuso, sgranchire, smacchiare, smacchiato, specchiato, specchiera, spocchioso, stracchino, succhiotto, tabacchino, vecchietto, vacchiezza, vecchiotto.
Parole di 11 lettere: accerchiare, accerchiato, acchiappare, acchiappato, accipicchia, ammucchiare, ammucchiato, bacchiatura, baldacchino, bianchiccio, bicchierino, birichinata, bofonchiare, catapecchia, chiacchiera, chiaramente, chiarimento, chiaroscuro, chiazzatura, chicchessia, chiesastico, chilogrammo, chitarrista, formichiere, ginocchiere, imbianchino, invecchiare, invecchiato, invischiare, invischiato, macchiaiolo, macchinario, macchinista, macchiolina, maschilismo, nevischiare, orecchiette, parchimetro, parrucchino, pastrocchio, pidocchioso, portachiavi, portapacchi, racchiudere, racchiusero, ridacchiare, rischiarato, schiacciare, schifiltoso, schiumogeno, schizzinoso, semicerchio, sfacchinare, sgranchirsi, socchiudere, specchietto, tabacchiera, torchiatura, vecchiaccio, vischiosità
Parole di 12 lettere: antichissimo, architettura, bagnoschiuma, bistecchiera, cannocchiale, canticchiare, chiavistello, cincischiare, dormicchiare, fattucchiera, fischiettare, furbacchiona, guardaboschi, impratichire, marchingegno, mattacchiona, montacarichi, mordicchiare, mordicchiato, nevischiando, occhiataccia, orsacchiotto, paraorecchie, parrucchiera, picchiatello, picchiettato, rannicchiato, rispecchiare, rispecchiato, schiamazzare, schiarimento, schieramento, schizofrenia, scoperchiare, scoperchiato, scribacchina, scricchiolio, smacchiatore, sonnacchioso, sonnecchiare, spidocchiare, tagliaboschi, vecchierello, vivacchiando
Parole di 13 lettere: acchiappacani, apparecchiare, apparecchiato, bruciacchiare, bruciacchiato, canticchiando, chiacchierare, chiacchierina, chiacchierona, chincaglieria, dormicchiando, infinocchiato, leggiucchiare, mangiucchiare, riacchiappare, rimorchiatore, sbaciucchiare, schiaccianoci, schifosaggine, volpacchiotto
Parole di 14 lettere: accerchiamento, ammonticchiare, ammonticchiato, chiaroveggente, chiaroveggenza, orecchiabilità, scarabocchiare, scarabocchiato, schiacciasassi, schiaffeggiare, schiaffeggiato, sottobicchiere.
____________________
E queste sono le schede a colori, pronte per il download e la stampa per gli abbonati:
Il materiale comprende:
Carte mute (solo immagini)
Cartellini in stampato minuscolo
Cartellini in corsivo
Nomenclature in stampato minuscolo
Nomenclature in corsivo
Carte mute (solo immagini)
Cartellini in stampato minuscolo
____________________
Cartellini in corsivo
_____________________
Nomenclature in stampato minuscolo
_____________________
Nomenclature in corsivo
_____________________
Qui alcuni dettati ortografici:
A corredo del progetto di insegnamento della corretta igiene orale ai bambini, ho preparato queste carte delle nomenclature in tre parti (illustrate con parola, solo illustrazione e solo parola) sulla struttura del dente.
Come già detto qui,
i bambini che già da molto piccoli hanno imparato a lavarsi i denti, presto desidereranno ricevere informazioni sui loro denti, sapere come si chiamano, come sono fatti, ecc… Per questo è importante predisporre per lui molte attività sul tema.
Imparare l’anatomia e la fisiologia dei denti aiuterà i bambini a lavarsi i denti ancora meglio, con maggior consapevolezza, e le prime informazioni possono essere date a partire dalla scuola d’infanzia.
Nella scuola primaria è poi importante riprendere ed approfondire coi bambini tutti i temi affrontati quando erano più piccoli, arricchendo le nozioni di anatomia e fisiologia di contenuti scientifici appropriati all’età.
Conoscere aumenta la motivazione a lavarsi bene i denti e favorisce l’indipendenza e l’autonomia.
Per l’uso delle carte delle nomenclature puoi leggere qui.
sono disponibili gratuitamente per gli abbonati qui:
Aggiungo uno schema riassuntivo, da utilizzare sempre coi cartellini:
Riferimenti all’argomento nel web:
– wholehealthsource.blogspot.com
– stepintosecondgrade.blogspot.com
Carte delle nomenclature per parole con consonanti doppie – Metodo Montessori. Come già detto per le carte delle nomenclature per parole di tre lettere
e per le carte delle nomeclature per parole di quattro lettere,
una volta che il bambino ha fatto molti esercizi di composizione di parole per dettatura con l’alfabeto mobile, è pronto per gli esercizi di autodettatura, cioè per comporre autonomamente parole che egli stesso ha pensato, senza averle sentite dalla voce di altri.
Esistono molte possibilità per favorire questo genere di esercizio, una può essere quella di preparare delle schede illustrate, che possono anche fornire un aiuto all’arricchimento del lessico.
Classicamente le carte delle nomenclature, a questo secondo scopo, sono organizzate per aree tematiche (animali domestici, casa, abbigliamento, mezzi di trasporto, ecc…).
Qui propongo una classificazione diversa, in funzione dell’apprendimento delle varie difficoltà ortografiche presenti nella nostra lingua: cominciamo con le consonanti doppie.
Carte delle nomenclature per parole con consonanti doppie – Metodo Montessori
Questo è una selezione di parole italiane che presentano consonanti doppie, con diversi gradi di difficoltà; non tutte si prestano ad essere illustrate e le parole presenti nelle schede delle nomenclature sono in grassetto:
anno asso asse inno osso otto
babbo bacca baffo basso becco beffa birra bocca bocce bolle botte botto bucce buffo burro canne carro cappa cassa ceppo colla collo coppa cotto cozze donna facce farro fatto fetta fibbia fisso fitto fosso gallo gatto gemma gobbo gocce gomma legge lesso letto lutto mamma mappa massa masso matto mazze messa mezzo mosso mozzo muffa notte nozze occhio pacco palla panna panno pappa passo pazzo penna pezza pinna Pippo pizza pizzo pollo porri pozza pozzo Puffo raggi razzo ressa retto ritto rocce rosso rotto sacco sassi secco sella senno serra sette sonno succo tacco tappo tassa tatto tazza terra tetto tocco tonno toppa torre tosse tuffo vacca valle villa zappa zoppo zucca zuppa
anello bacche becchi bocche brocca brutto buccia caccia cuccia cuffia doppio dubbio faccia faggio fiocco frecce gabbia giacca gnocchi goccia graffio grappa grasso grosso grotta grucce fiamma labbra loggia maggio mummia nebbia nibbio pacchi paggio peggio piazza pioppo poggio rabbia raggio reggia riccio sabbia sacchi saggio sbarra sbuffo scatto seppia soffio spalla spilla staffa stalla stella stemma tacchi tracce tratto treccia trippa trotto trucco vacche
accappatoio antenna allegro arrosto astuccio barella bicicletta braccio breccia bocciolo bottiglia bottoni brocche burrone bussola cammello cannone capanna cappello caraffa carrelli cartella cartello casetta castello cestello ciabatta colonne chitarra collana collare collina coltello cordicella cravatta dattero fagotto fessura fiammiferi formaggio freccia frittata fumetti gallina gemelli giraffa ghiaccio grappolo greppia gruccia lattuga lettera lucciola maglietta mantello marrone matassa materassi mattarello mattone mollica occhiali ombrello padella paletta paletto pallina pallone pattini pennello pestello pettine picchio piffero pillola pioggia pittura pollice polline quattro raganella ramarro rametto rastrello sassolino scaffale scoppio spaccio spaghetti spazzola specchi spiaggia spicchio spiccio sprazzo spruzzo stampelle straccio strenna stretto tacchino tallone terreno traccia trebbia treccia trombetta trottola tinello vassoio viaggio vitello zafferano zucchero.
E queste sono le carte a colori, pronte per il download e la stampa per gli abbonati:
(Per sapere come utilizzarle puoi fare riferimento al post Schede delle nomenclature per parole di tre lettere).
Raccomando, naturalmente, di non presentare al bambino le schede tutte insieme, ma di selezionarne circa una decina alla volta…)
Memory Italiano-Inglese – Per preparare la lettura e la scrittura delle parole in Inglese ho preparato questo memory casalingo.
Se volete prepararlo anche voi alla stesso modo, stampate due volte il materiale:
Le coppie di immagini si incollano su due cartoncini di colore diverso, io ho scelto rosa e azzurro. Poi sotto a quello rosa ho scritto la parola in corsivo in Italiano (il corsivo lo stiamo proprio imparando in questi giorni), e sotto a quello azzurro la parola in stampato minuscolo in Inglese.
Girando le carte i bambini leggono le parole, quindi formano le coppie.
Se vi può essere utile, aggiungo anche le schede già pronte, nella versione Italiano-Inglese, solo Italiano, solo Inglese, che possono essere usate come le carte delle nomenclature Montessori
Schede per il riconoscimento delle erbe del prato – Ho realizzato tempo fa queste schede illustrate per il riconoscimento delle erbe selvatiche più comuni per una seconda classe, dopo aver lavorato coi dettati ortografici sulle erbe del prato,
avviando anche le prime raccolte di erbe per la produzione di un erbario di classe.
Il livello di approfondimento è adeguato all’età. I nomi latini sono importanti, accanto al nome volgare, per ricercare ulteriori informazioni relative a quella specifica erba; non se ne richiede certo la memorizzazione :-)… e lo stesso vale per la classificazione botanica.
Queste sono le schede per il riconoscimento delle erbe del prato:
che puoi scaricare in formato pdf qui:
Istruzioni per le schede per il riconoscimento delle erbe del prato: ogni foglio contiene la scheda fronte-retro di due erbe del prato. Ritagliate dunque due strisce orizzontali da ogni foglio, e ripiegatele lungo la linea verticale al centro. La scheda può essere plastificata così a doppio, oppure l’interno può essere utilizzato per conservare i campioni di erbe raccolte e per le annotazioni.
Per un lavoro più approfondito le risorse migliori che ho trovato nel web, tutte gratuite, sono queste:
le schede botaniche illustrate da Carl Axel Magnus Lindman
http://caliban.mpiz-koeln.mpg.de/lindman/
le schede botaniche illustrate da Otto Wilhelm Thomé
http://www.biologie.uni-hamburg.de/b-online/thome/Alphabetical_list.html
una raccolta di link ad altre risorse:
http://www.floramedica.org/page7.htm
raccolte da cui ho tratto le immagini per realizzare le schede.
Metodo Montessori – schede delle nomenclature per parole di quattro lettere. Come già detto per le schede delle nomenclature per parole di tre lettere,
una volta che il bambino ha fatto molti esercizi di composizione di parole per dettatura con l’alfabeto mobile, è pronto per gli esercizi di autodettatura, cioè per comporre autonomamente parole che egli stesso ha pensato, senza averle sentite dalla voce di altri.
Esistono molte possibilità per favorire questo genere di esercizio, una può essere quella di preparare delle schede illustrate, che possono anche fornire un aiuto all’arricchimento del lessico.
Classicamente le schede delle nomenclature, a questo secondo scopo, sono organizzate per aree tematiche (animali domestici, casa, abbigliamento, mezzi di trasporto, ecc…). Qui propongo una classificazione diversa, per lunghezza della parola, e dopo aver proposto un elenco di parole di tre lettere, passo a quelle di quattro.
____________________
Metodo Montessori – schede delle nomenclature per parole di quattro lettere
Questo è una selezione di parole italiane di quattro lettere, ma non tutte si prestano ad essere illustrate; le parole presenti nelle schede delle nomenclature sono in rosso:
acca, acme, acne, acre, Adda, afta, aghi, agio, agli, alba, albo, alce, alga, Alma, aloe, alpe, alto, ambo, amen, anca, anno, Anna, ansa, anta, arca, arco, area, aria, arma, arpa, asso, asse, asta, Asti, ateo, atto, aula, aura, auto
baci, baco, baia, baio, bara, baro, base, bava, bebè, bene, beni, bere, bici, biga, bile, biro, boia, bolo, bora, boro, bove, brio, buca, buco, buio, buoi,
caco, Caio, calo, cane, caos, capo, cara, casa, caso, cava, cavo, ceci, cena, cera, cero, ceto, ciao, cibo, cima, Ciro, coda, coma, Como, cono, coro, cosa, cova, cubo, cupo, cura, cute,
dado, dama, dare, data, dato, diga, Dino, dire, dito, diva, doga, doge, dolo, dono, dopo, Dora, dose, dote, dove, duca, duce, duna, duro,
ecco, Egeo, eden, echi, elfo, Elia, elmo, elsa, emme, Enea, Enna, enne, ente, eone, equo, erba, ergo, eroe, erre, erta, esca, etto, euro,
falò, fama, fame, faro, fase, fata, fava, favo, fede, fedi, fesa, feta, fico, fido, fifa, fila, filo, foro, foto, fuco, fuga, fumo, fune, fuso
Gaia, gaio, gala, gara, geco, gelo, gene, giga, giro, gita, gnam, gola, golf, gong, gres, guai, gufo, guru,
iato, ibis, idea, idem, iena, ieri, inca, inno, iosa, iris, irta, isba, iuta,
lago, lama, lana, lato, lava, lega, lego, lena, leso, leva, lido, lima, limo, lino, lira, lite, lobo, lode, loto, luce, lume, luna, lupo,
mago, mais, male, mano, mare, maso, mela, melo, meno, menù, mese, meta, metà, miao, mimo, mina, Mino, mira, mola, mole, molo, mora, mota, moto, muco, mulo, muro, musa, muso, muto,
nano, naso, nato, nave, neon, nero, neve, nido, Nino, noce, nodo, noia, nolo, nome, nono, nord, nota, nove, nube, nuda, nume,
oasi, oblò, oboe, oche, ocra, odio, oggi, ogni, olio, olmo, onda, onta, orba, orca, orco, orda, orlo, orma, orso, orto, orzo, osso, oste, otre, otto, ozio
pace, paga, paio, pala, palo, pane, papa, papà, pari, pece, pelo, pena, pepe, pera, pero, pesa, peso, pila, pino, pipa, pira, poco, polo, pomo, posa,
quiz
rado, ragù, rame, ramo, rana, rapa, rara, rasa, raso, rata, remo, rena, rene, reso, rete, riga, rima, riso, riva, roba, rogo, rosa, rovo, rude, ruga, runa, rupe, ruta,
saga, saio, sala, sale, sana, Sara, scia, sebo, sede, sega, seme, sera, seta, sete, sito, smog, soci, soda, sofà, soia, sole, soma, spia, stop, sugo,
tana, tara, tata, taxi, teca, tela, telo, tema, tesa, tesi, tifo, timo, Tina, tino, tipo, tiro, toga, tomo, tono, topo, toro, tram, trio, tris, tubo, tufo, tuta, tutù,
ulna, unno, unto, uomo, uovo, urlo, urna, urto,
vago, vano, varo, vaso, vela, velo, vena, vera, veto, vice, vile, vino, viso, vite, vivo, vizi, voce, voga, volo, voto,
yoga
Zara, zebù, zelo, zero, zeta, zona, zulu.
Metodo Montessori – schede delle nomenclature per parole di quattro lettere
E queste sono le schede a colori, pronte per il download e la stampa per gli abbonati:
Il materiale comprende:
– carte mute (solo immagine)
– carte immagine + nome in stampato minuscolo
– carte immagine + nome in corsivo.
Metodo Montessori – nomenclature mute Montessori parole di quattro lettere
(sono le schede illustrate, senza nomi)
Metodo Montessori – nomenclature Montessori parole di quattro lettere stampato minuscolo
________________________________
Metodo Montessori – nomenclature Montessori parole di quattro lettere corsivo
Carte delle nomenclature Montessori per parole di tre lettere – una volta che il bambino ha fatto molti esercizi di composizione di parole per dettatura con l’alfabeto mobile, è pronto per gli esercizi di autodettatura, cioè per comporre autonomamente parole che egli stesso ha pensato, senza averle sentite dalla voce di altri.
Esistono molte possibilità per favorire questo genere di esercizio, una può essere quella di preparare delle schede illustrate, che possono anche fornire un aiuto all’arricchimento del lessico. Classicamente le schede delle nomenclature, a questo secondo scopo, sono organizzate per aree tematiche (animali domestici, casa, abbigliamento, mezzi di trasporto, ecc…). Qui propongo una classificazione diversa, per lunghezza della parola, cominciando dalle parole di tre lettere.
Questo è una selezione di parole italiane di tre lettere di senso compiuto, ma non tutte si prestano ad essere illustrate:
afa, ago, aia, ala, amo, ape,
bar, bue, bus, blu, boa,
dio, due,
eco, est, Eva,
gel, gol, gru, gnu,
ira
Lea, lei, lui,
mia, mio, mie,
nel, neo, non, Noè,
oca, ode, ora, oro,
per, più, pio, poi, può,
qua, que, qui,
sai, sei, sax, sia, sua, sub, sud, sue, sul, suo,
tra, tre, tua, tuo,
ufo, uno, uva,
vai, via
yak
zar, zia, zio, zii, zoo.
E queste sono le schede a colori, pronte per il download e la stampa:
Come possiamo utilizzare le carte delle nomenclature Montessori (a casa ho solo una stampante in bianco e nero, ma le schede sono a colori):
1. per i soli esercizi di autodettatura, possiamo stampare una copia delle schede, nel carattere scelto per l’alfabeto mobile (corsivo o stampato minuscolo), ritagliare e ripiegare la parte che contiene la parola scritta. In questo modo il bambino può comporre la parola guardando l’immagine, e in seguito controllare il suo lavoro girando la carta:
2. per i classici esercizi di nomenclatura, stampare due copie del carattere scelto, ritagliare e se volete plastificare. Lasciare per ogni coppia di schede uguali una copia intera (immagine e parola, “scheda parlata”) e una separata (ritagliare l’immagine e la parola a parte, “scheda muta”).
Sarebbe meglio incollare le schede su due cartoncini di uguale dimensione, soprattutto per i bambini più piccoli. Sono in fase di preparazione varie schede delle nomenclature appositamente fatte in tre parti, se volete aspettare…
Mettere tutto in una cartellina o una busta, a disposizione del bambino. Il bambino porterà la cartellina su un tappeto abbastanza grande, e comincerà disponendo in basso a destra la pila di schede mute, la pila di schede parlate, e i cartellini.
Quindi, partendo dalla parte del tappeto in alto a sinistra, dispone una sotto l’altra tutte le schede mute, formando una fila verticale.
Quindi prende una ad una le schede parlate, e una ad una le dispone a destra delle schede mute corrispondenti. In ultimo posiziona i cartellini.
3. L’esercizio di nomenclatura può essere variato preparando schede parlate in stampato minuscolo, e schede mute coi cartellini in corsivo (o viceversa), per l’appaiamento carattere stampato – corsivo.
DIVISIONE IN SILLABE – schede: i bambini hanno a disposizione in classe una scatola-schedario di esercizi vari per ogni materia, da scegliere liberamente, che è uno per tutti: abbiamo per cominciare uno schedario per la Matematica, uno per l’Italiano, uno per la Musica e uno per l’Inglese.
Ogni bambino ha poi una scatola-schedario individuale, col suo nome, dove conserva i cartellini che ha usato per i suoi esercizi. E’ assurdo incollare fotocopie su fotocopie sui quaderni! Questa modalità favorisce il lavoro individuale e individualizzato, ma anche l’aiuto reciproco e la collaborazione: se un bambino ha già provato un dato esercizio, può dare una mano al compagno che lo sta facendo; poi ci sono anche schede per lavorare in coppia, ad esempio quelle dei dettati che prevedono che un bambino legga al bambino che scrive.
E’ naturalmente sempre il bambino a scegliere; se lo desidera può portare anche il lavoro a casa: vi sembrerà assurdo, ma a me che non uso dare compiti, i bambini li chiedono…
A differenza degli eserciziari “a libro”, lo schedario mi permette di aggiornare l’offerta di esercizi in base agli interessi dei bambini, o alle difficoltà che mostrano, e inoltre si integra benissimo coi materiali montessoriani già a disposizione.
Cominciamo con le schede per esercitare la divisione in sillabe.
__________________________
DIVISIONE IN SILLABE – REGOLE
Le regole della nostra lingua non sono affatto semplici, ricordiamole:
– una vocale a inizio parola, seguita da una sola consonante, fa sillaba a sè: a-nima, i-sola, o-livo
– le consonanti semplici fanno sillaba con la vocale che segue: li-mo-na-ta, se-re-ni-tà
– le consonanti doppie di dividono in due sillabe: pez-zet-ti-no, am-mat-ti-re; rientrano tra le doppie le parole con cqu: ac-qua, ac-quisto, nac-que
– due o tre consonanti diverse tra loro (non doppie) fanno sillaba con la vocale seguente, se esistono come gruppo anche all’inizio delle parole: a-bra-sivo ( perchè br esiste come inizio di parole, ad esempio in brina), ca-tra-me (treno), pu- le -dro (dritto),
– la esse impura (s seguita da consonanti) si attacca alla sillaba: e-scludo, ma-stino
– quando il gruppo di consonanti non esiste come inizio di parole, la prima consonante si stacca dalla sillaba: arit- metica (tme), pal-ma (lm), bam-bino (mbi),
– dittonghi e trittonghi non si possono dividere (au, ia, …), a meno che non si tratti di uno iato (ma meglio prendere la regola come generale, per non sbagliare, perchè ad esempio pi-o-lo è giusto, ma non si può fare pi-o-ve; allora meglio pio-lo pio-ve)
– digrammi e trigrammi non di dividono mai (sc, gl, gn,…)
– l’apostrofo in fin di riga è ammesso.
I bambini piccoli naturalmente imparano molto meglio a ricoscere la sillaba e quindi a dividere correttamente, seguendo la musicalità dei suoni e facendo esercizio. Ad esempio quando devono andare a capo insegniamo loro a dire la parola a voce alta battendo forte le mani ad ogni interruzione di sillaba: non sbagliano quasi mai!
___________________________________
DIVISIONE IN SILLABE – Ecco le schede, se possono esservi utili:
_____________________________________
Questo è il contenuto delle schede:
Dividi in sillabe:
rosa vaso rame casa nove mare lama tino pipa rana rapa seme
Ro-sa Va-so Ra-me Ca-sa No-ve Ma-re La-ma Ti-no Pi-pa Ra-na Ra-pa Se-me
pino tara caro sodo pila meno tana rupe palo pera sale luna vino
Pi-no Ta-ra Ca-ro So-do Pi-la Me-no Ta-na Ru-pe Pa-lo Pe-ra Sa-le Lu-na Vi–no
naso zero foglia vite libro uva pietra pane treno mosto campo orto fiori
Na–so Ze–ro Fo–glia vi-te li-bro u–va pie–tra pa–ne tre–no mo–sto cam–po or–to fio–ri
mamma palla masso tazza asse mazza pollo prezzo pazzo nonno pezza colla razzo
Mam–ma pal–la mas–so taz–za as–se maz–za pol–lo prez–zo paz–zo non–no pez–za col–la raz-zo
pozzo carro nonna cavallo carrozza fazzoletto mezza notte pallottola gallina mazzetto collina caramella
Poz-zo Car-ro Non-na Ca–val-lo Car–roz-za Faz–zo–let-to Mez-za Not-te Pal–lot–to-la Gal–li-na Maz–zet-to Col-li-na Ca–ra–mel-la
ciclismo cieco ladro mascella mondo ospedale orso placca prosciutto qualcuno romanzo simpatia spingere
Ci–cli-smo cie-co la-dro ma–scel- la mon-do o-spe-da-le or-so plac-ca pro-sciut-to qual–cu-no ro-man-zo sim-pa-ti-a spin–ge-re
idea adagio bordo balbettare badia balestra balsamo bambola balneare batticuore bavaglino beato biglia biforcuto biliardo bimbo bilancia
i–de-a a–da-gio bor-do bal-bet-ta-re ba-di-a ba-le-stra bal–sa-mo bam- bo-la bal–ne–a-re bat–ti–cuo-re ba–va–gli-no be–a-to bi–glia bi-for-cu-to bi-liar-do bim-bo bi-lan-cia
idrante archetto arachide arbitrio aprile arte attraente attrezzo avaro avverbio avventura avvoltoio azione azzuffarsi bagaglio bagnare baia
i–dran-te ar–chet-to a-ra-chi-de ar–bi-trio a-pri-le ar-te at–tra–en-te at–trez-zo a–va-ro av–ver-bio av–ven-tu-ra av–vol–to-io a–zio–ne az–zuf–far-si ba–ga-glio ba–gna-re ba-ia
appunto bitorzolo bisonte birichino blindato bivio boato boccaglio bomba bolgia borghese borsa bottiglia branzino briciola briglia brodo
ap–pun-to bi–tor–zo-lo bi–son-te bi-ri-ch-no blin-da-to bi-vio bo–a-to boc–ca-glio bom-ba bol-gia bor-ghe-se bor-sa bot-ti–glia bran–zi-no bri-cio-la bri-glia bro-do
bisbetica buono buongustaio buonora buonsenso burla calcagno calce calendario calligrafia calzamaglia
bi-sbe-ti-ca buo-no buon-gu–sta-io buo–no-ra buon-sen-so bur-la cal–ca-gno cal-ce ca–len–da-rio cal–li–gra-fia cal-za–ma-glia
cambio calzetta camoscio camicia campanel la campagna candeggi na canguro canto canzone bacio
cam-bio cal–zet-ta ca–mo-scio ca–mi-cia cam–pa-nel-la cam–pa-gna can-deg-gi-na can-gu-ro can-to can–zo-ne ba-cio
capretto capsula carbone carnivoro cartella casalinga catechismo catasto catrame cattedra brutto
ca–pret-to cap–su-la car-bo-ne car-ni-vo-ro car–tel-la ca-sa–lin-ga ca–te-chi-smo ca–ta-sto ca-tra-me cat–te-dra brut-to
cattiveria cattedrale catenaccio causa cauzione cavalcare cavalletto caviglia cavia cavolfiore celeste celebre cencio cemento
Cat-ti-ve-ria cat-te–dra-le ca–te–nac-cio cau-sa cau–zio-ne ca-val–ca-re ca–val–let-to ca–vi-glia ca-via ca–vol–fio-re ce–le-ste ce–le-bre cen-cio ce–men-to
centro centesimo cento cerimonia ceramista cervello certificato chiara chiamare cestino chiave chicco chiedere chiesa
Cen-tro Cen–te–si-mo Cen-to Ce-ri–mo-nia Ce–ra–mi- sta Cer–vel-lo Cer–ti–fi–ca-to Chia-ra Chia–ma-re Ce-sti-no Chia-ve chic-co chie-de-re chie-sa
chilometro chissà chiocciola chiosco chirurgo chitarra chiuso ciao cialda ciambella cigno ciclismo cicogna ciecamente
Chi-lo–me-tro chis-sà chioc-cio-la chio-sco chi–rur-go chi-tar-ra chiu-so cia-o cial-da ciam-bel-la ci-gno ci–cli-smo ci–co-gna cie–ca–men te
cicogna cifra cielo ciclone cilindro ciliegia ciminie ra cinghia cinquanta cipresso cintura circolare civiltà cisterna classe clessidra cliente
ci-co-gna ci-fra cie-lo ci–clo-ne ci–lin-dro ci–lie-gia ci–mi–nie-ra cin-ghia cin–quan-ta ci–pres-so cin-tu-ra cir–co–la-re ci–vil-tà ci-ster-na clas-se cles–si-dra cli–en-te
cobra coccinella cognome colbacco collaudo collegio colmo coltivare combattimento commedia commessa compagnia compagno compatto compito composto condividere
co-bra coc-ci-nel-la co–gno-me col–bac-co col–lau-do col–le-gio col-mo col-ti–va-re com–bat–ti–men-to com–me-dia com–mes-sa com-pa-gnia com-pa-gno com-pat-to com-pi-to com–po-sto con-di-vi-de-re
confettura confine congelare coniglio conoscenza consiglio conquista consegna consenso conserva contato contento conto convento coppa coprire cooperativa
Con–fet–tu-ra Con–fi-ne Con–ge–la-re Co–ni-glio co–no–scen-za con-si-glio con-qui-sta con-se-gna con–sen-so con–ser-va con–ta-to con-ten-to con-to con-ven-to cop-pa co-pri-re co–o–pe-ra-ti-va
coordinarecoperta copia coprifuoco copriletto coraggio corda cordialità coriandolo cornacchia cornetto cornuto corpo correggere corrente corridoio cortesia
Co – or – di – na – reCo – per – taco – pia co – pri – fuo – co co – pri – let – to co – rag – gio cor- da cor – dia – li- tà co – rian – do – lo cor- nac – chia cor – net – to cor – nu – to cor – po cor – reg – ge – re cor – ren – te cor – ri – do – io cor –te – sia
coscienza coscia costo cosmetico costare crampo costume cratere crauti cranio creato creare creatività crescita cristallo crimine critica
Co–scien-za co-scia co-sto cos–me-ti-co co–sta-re cram-po co–stu-me cra-te-re crau-ti cra-nio cre-a-to cre-a-re crea-ti-vi-tà cre–sci-ta cri–stal-lo cri-mi-ne cri–ti-ca
criticone crostata crudo culmine culto cuore acquarello curiosità dalmata cuscinetto dentista danzare dardo dattero davanti degradabile decenza
cri-ti–co-ne cro–sta-ta cru-do cul-mi-ne cul-to cuo-re ac–qua–rel-lo cu-rio-si-tà dal–ma-ta cu–sci–net-to den–ti-sta dan-za-re dar-do dat-te-ro da–van-ti de–gra–da-bi-le de-cen-za
dente deserto desiderio diabolico deviazione diamante dicembre dettaglio diabete dialogare diplomazia discesa discorso distanza domanda
Den-te de–ser-to de-si-de-rio dia–bo–li-co de-via–zio-ne dia–man-te di-cem-bre det-ta-glio dia-be-te dia–lo–ga-re di–plo–ma-zia di-sce-sa di-scor-so di-stan-za do–man-da
fango fauna febbraio fat toria ferragosto fiamma fiaba filastrocca firmamento fiocco finta fosforescente foschia fraterno francobollo
fan-go fau-na feb–bra-io fat-to-ri-a fer–ra–go-sto fiam-ma fia-ba fi-la–stroc-ca fir–ma–men-to fioc-co fin-ta fo-sfo-re-scen-te fo–schi-a fra-ter-no fran-co–bol-lo
frangia frullino frusta fronte frutta galassia gaiezza geranio genio gente gioire gioioso gioco giocattolo gonnellina
Fran-gia Frul-li-no Fru-sta Fron-te frut-ta ga–las-sia ga–iez-za ge–ra-nio ge-nio gen-te gio-i-re gio-io-so gio-co gio–cat–to-lo gon–nel-li-na
grattugia granello guardaroba guscio guida guinzaglio illustrazione imballa re imburrato i mitare impegno incantesimo infarinare insetto insegnare
grat-tu-gia gra–nel-lo guar–da–ro-ba gu-scio gui-da guin–za-glio il–lu–stra–zio-ne im–bal–la-re im-bur-ra-to i-mi-ta-re im–pe-gno in-can-te–si-mo in–fa-ri–na-re in-set-to in–se–gna-re
lastra levante lezione lineamenti lingua lungo maestra maestà magnetico magro maiuscolo maltempo marea margine marmellata
la-stra le–van-te le–zio-ne li–nea–men-ti lin-gua lun-go ma–e-stra mae-stà ma-gne-ti-co ma-gro ma–iu–sco-lo mal–tem-po ma–re-a mar-gi-ne mar–mel–la-ta
marinaio maschera mastello materia meglio metropolitana microfono migliaio miscela miseria moderno molla monte montante movimento mungere
Ma-ri–na-io Ma–sche-ra ma–stel-lo ma–te-ria me-glio me–tro-po-li-ta-na mi–cro–fo-no mi–glia-io mi-sce-la mi-se-ria mo-der-no mol-la mon-te mon-tan-te mo-vi–men-to mun-ge-re
nascere nastrino nascondino neolitico neonato nervoso nucleo obliquo oculista olivo ombelico ombrellone opposto opuscolo oriente organo
na-sce-re na-stri-no na–scon-di-no neo-li-ti-co neo-na-to ner-vo-so nu-cleo o-bli-quo o–cu-li-sta o-li-vo om–be-li-co om-brel-lo-ne op-po-sto o-pu-sco-lo o-rien-te or-ga-no
pannocchia pappagallo parte percussione pestifero piano placca polmonite portafortuna pozzanghera prefisso privato proibito promessa proprio
Pan-noc-chia pap-pa–gal-lo par-te per–cus-sio-ne pe-sti-fe-ro pia-no plac-ca pol-mo-ni-te por-ta-for-tu-na poz-zan–ghe-ra pre-fis-so pri–va-to proi-bi-to pro-mes-sa pro-prio
pugno pulpito pulizia qualifica quantità questione quiete raccolta raddoppiare rampicante reagire realista richiamo rischio risposta ruota
pu-gno pul-pi-to pu-li-zia qua-li-fi-ca quan-ti-tà que–stio-ne qui–e-te rac–col-ta rad-dop-pia-re ram-pi–can-te rea-gi-re rea-li-sta ri-chia-mo ri-schio ri-spo-sta ruo-ta
saldare scegliere scarto sciacquare segmento società sospirare stringa tecnologia terzo tombino trofeo ultimo unghia urlo utile
sal–da-re sce-glie-re scar-to sciac-qua-re seg–men-to so-cie-tà so–spi-ra-re strin-ga tec-no-lo-gia ter-zo tom–bi-no tro-fe-o ul-ti-mo un-ghia ur-lo u-ti-le
vario verso vetro vigneto volante zaino zucchero zoppicare zenzero zampone zafferano vuoto vulcano vostro versare vaglia
va-rio ver-so ve-tro vi-gne-to vo–lan-te zai-no zuc-che-ro zop-pi-ca-re zen-ze-ro zam-po-ne zaf–fe-ra-no vuo-to vul-ca-no vo-stro ver-sa-re va-glia
_________________________________
Sul retro, dove ci sono le soluzioni per la correzione e l’autocorrezione, pinzo un foglietto, così prima di riporre la scheda il bambino può mettere la sua firma. E poi fa un po’ da “tenda del mistero”…
E' pronto il nuovo sito per abbonati: la versione Lapappadolce che offre tutti i materiali stampabili scaricabili immediatamente e gratuitamente e contenuti esclusivi. Non sei ancora abbonato e vuoi saperne di più? Vai qui!
